“绿色出行,低碳健身”已成为广大市民的共识.某旅游景点新增了一个公共自行车停车场,6:00至18:00市民可在此借用自行车,也可将在各停车场借用的自行车还于此地.林华同学统计了周六该停车场各时段的借、还自行车数,以及停车场整点时刻的自行车总数(称为存量)情况,表格中x=1时的y值表示7:00时的存量,x=2时的y值表示8:00时的存量…依此类推.他发现存量y(辆)与x(x为整数)满足如图所示的一个二次函数关系.
根据所给图表信息,解决下列问题:
(1)m= ,解释m的实际意义: ;
(2)求整点时刻的自行车存量y与x之间满足的二次函数关系式;
(3)已知9:00~10:O0这个时段的还车数比借车数的3倍少4,求此时段的借车数.
已知:如图,已知△ABC,
(1)画出与△ABC关于 轴对称的图形△A1B1C1.
轴对称的图形△A1B1C1.
(2)求△ABC的面积.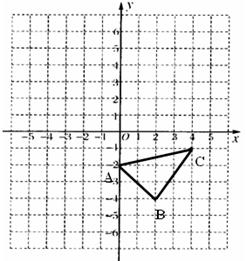
已知 和
和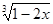 互为相反数,求
互为相反数,求 的值.
的值.
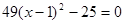
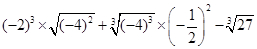 .
.
平面内的两条直线有相交和平行两种位置关系.
(1)AB∥CD.如图a,由AB∥CD,有∠B=∠BOD,又因∠BOD是△POD的外角,故∠BOD=∠BPD +∠D,得∠BPD+∠D=∠B.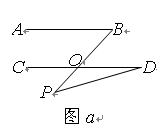
如图b,以上结论是否成立?若不成立,则∠BPD、∠B、∠D之间有何数量关系?请说明理由; 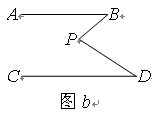
(2)在图b中,将直线AB绕点B逆时针方向旋转一定角度交直线CD于点E,如图c,则∠BPD﹑∠B﹑∠D﹑∠BED之间有何数量关系?(不需说明理由);
(3)根据(2)的结论求图d中∠A+∠B+∠C+∠D+∠E+∠F的度数.