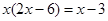三个小球分别标有﹣2,0,1三个数,这三个球除了标的数不同外,其余均相同,将小球放入一个不透明的布袋中搅匀.
(1)从布袋中任意摸出一个小球,将小球上所标之数记下,然后将小球放回袋中,搅匀后再任意摸出一个小球,再记下小球上所标之数,求两次记下之数的和大于0的概率.(请用“画树状图”或“列表”等方法给出分析过程,并求出结果)
(2)从布袋中任意摸出一个小球,将小球上所标之数记下,然后将小球放回袋中,搅匀后再任意摸出一个小球,将小球上所标之数再记下,…,这样一共摸了13次.若记下的13个数之和等于﹣4,平方和等于14.求:这13次摸球中,摸到球上所标之数是0的次数.
如图,AC是⊙O的直径,点B,D在⊙O上,点E在⊙O外,∠EAB=∠D=30°.
(1)求证:AE是⊙O的切线;
(2)当AB=3时,求图中阴影部分的面积(结果保留根号和π).
已知关于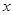 的一元二次方程
的一元二次方程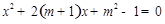 .
.
(1)若方程有实数根,求实数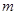 的取值范围;
的取值范围;
(2)若方程两实数根分别为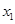 ,
,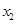 ,且满足
,且满足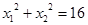 ,求实数
,求实数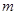 的值
的值
已知:△ABC在直角坐标平面内,三个顶点的坐标分别为A(0,3)、B(3,4)、C(2,2)(正方形网格中每个小正方形的边长是一个单位长度).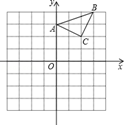
(1)画出△ABC向下平移4个单位长度得到的△A1B1C1,点C1的坐标是 ;
(2)以点B为位似中心,在网格内画出△A2B2C2,使△A2B2C2与△ABC位似,且位似比为2:1,点C2的坐标是 ;
(3)△A2B2C2的面积是 平方单位.
小明与甲、乙两人一起玩“手心手背”的游戏.他们约定:如果三人中仅有一人出“手心”或“手背”,则这个人获胜;如果三人都出“手心”或“手背”,则不分胜负,那么在一个回合中,如果小明出“手心”,则他获胜的概率是多少?(请用“画树状图”或“列表”等方法写出分析过程)
解方程:
(1)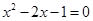 (用配方法)
(用配方法)
(2)