我国是水资源匮乏的国家为鼓励节约用水,某市打算出台一项水费政策措施,规定:每一季度每人用水量不超过5吨时,每吨水费收基本价1.3元;若超过5吨而不超过6吨时,超过部分水费加收200%;若超过6吨而不超过7吨时,超过部分的水费加收400%,如果某人本季度实际用水量为 吨,应交水费为
吨,应交水费为 。
。
(1)求 、
、 、
、 的值;
的值;
(2)试求出函数 的解析式。
的解析式。
已知数列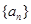 满足:
满足: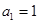 ,
,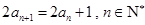 .数列
.数列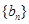 的前
的前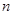 项和为
项和为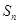 ,
,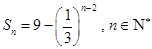 .
.
(Ⅰ)求数列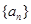 ,
,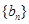 的通项公式;
的通项公式;
(Ⅱ)设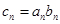 ,
,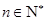 .求数列
.求数列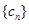 的前
的前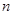 项和
项和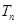 .
.
已知某几何体的直观图和三视图如下图所示,其正视图为矩形,侧视图为等腰直角三角形,俯视图为直角梯形.
(1)证明:BN⊥平面C1B1N;
(2)求点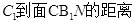
成都市海关对同时从A,B,C三个不同地区进口的某种商品进行抽样检测,从各地区进口此种商品的数量(单位:件)如表所示.工作人员用分层抽样的方法从这些商品中共抽取6件样品进行检测.
| 地区 |
A |
B |
C |
| 数量 |
50 |
150 |
100 |
(1)求这6件样品中来自A,B,C各地区商品的数量;
(2)若在这6件样品中随机抽取2件送往甲机构进行进一步检测,求这2件商品来自相同地区的概率.
本小题满分12分)已知函数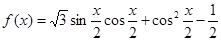 ,
,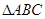 三个内角
三个内角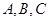 的对边分别为
的对边分别为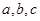 .
.
(Ⅰ)求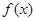 的单调递增区间及对称轴的方程;
的单调递增区间及对称轴的方程;
(Ⅱ)若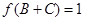 ,
,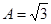
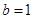 ,求角
,求角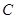 的大小.
的大小.
设函数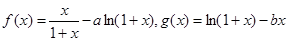 .
.
(1)若函数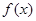 在
在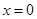 处有极值,求函数
处有极值,求函数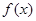 的最大值;
的最大值;
(2)是否存在实数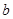 ,使得关于
,使得关于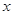 的不等式
的不等式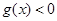 在
在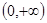 上恒成立?若存在,求出
上恒成立?若存在,求出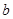 的取值范围;若不存在,说明理由;
的取值范围;若不存在,说明理由;
(3)记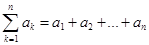 ,证明:不等式
,证明:不等式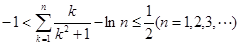 .
.