(本小题满分12分)已知直线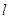 经过两条直线
经过两条直线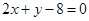 和
和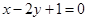 的交点.
的交点.
(1)若直线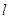 平行于直线
平行于直线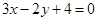 ,求直线
,求直线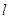 的方程;
的方程;
(2)若直线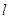 垂直于直线
垂直于直线 ,求直线
,求直线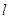 的方程.
的方程.
已知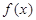 是定义在
是定义在 上的奇函数,当
上的奇函数,当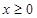 时,
时,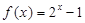 .
.
(1)求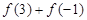 ;
;
(2)求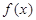 的解析式;
的解析式;
(3)若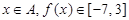 ,求区间
,求区间 .
.
对于函数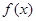 ,若存在实数对(
,若存在实数对(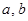 ),使得等式
),使得等式 对定义域中的每一个
对定义域中的每一个 都成立,则称函数
都成立,则称函数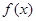 是“(
是“(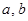 )型函数”.
)型函数”.
(1) 判断函数 是否为 “(
是否为 “(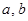 )型函数”,并说明理由;
)型函数”,并说明理由;
(2) 若函数 是“(
是“(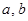 )型函数”,求出满足条件的一组实数对
)型函数”,求出满足条件的一组实数对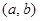 ;
;
(3)已知函数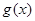 是“
是“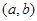 型函数”,对应的实数对
型函数”,对应的实数对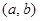 为
为 ,当
,当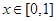 时,
时, ,若当
,若当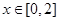 时,都有
时,都有 ,试求
,试求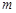 的取值范围.
的取值范围.
已知函数 .
.
(1)若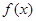 在
在 处取得极值,求
处取得极值,求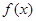 的单调递增区间;
的单调递增区间;
(2)若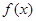 在区间
在区间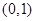 内有极大值和极小值,求实数
内有极大值和极小值,求实数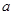 的取值范围.
的取值范围.
函数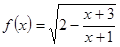 的定义域为
的定义域为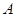 ,
, .
.
(1)求集合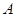 ;
;
(2)若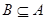 ,求实数
,求实数 的取值范围.
的取值范围.
命题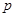 :关于
:关于 的不等式
的不等式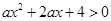 对一切
对一切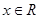 恒成立,命题
恒成立,命题 :函数
:函数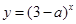 是增函数,若
是增函数,若 中有且只有一个为真命题,求实数
中有且只有一个为真命题,求实数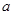 的取值范围.
的取值范围.