若有穷数列 (
(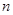 是正整数),满足
是正整数),满足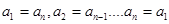 即
即 (
(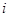 是正整数,且
是正整数,且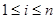 ),就称该数列为“对称数列”。
),就称该数列为“对称数列”。
(1)已知数列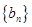 是项数为7的对称数列,且
是项数为7的对称数列,且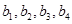 成等差数列,
成等差数列,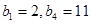 ,试写出
,试写出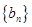 的每一项
的每一项
(2)已知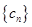 是项数为
是项数为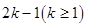 的对称数列,且
的对称数列,且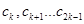 构成首项为50,公差为
构成首项为50,公差为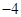 的等差数列,数列
的等差数列,数列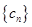 的前
的前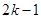 项和为
项和为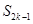 ,则当
,则当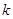 为何值时,
为何值时,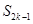 取到最大值?最大值为多少?
取到最大值?最大值为多少?
(3)对于给定的正整数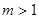 ,试写出所有项数不超过
,试写出所有项数不超过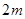 的对称数列,使得
的对称数列,使得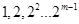 成为数列中的连续项;当
成为数列中的连续项;当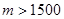 时,试求其中一个数列的前2008项和
时,试求其中一个数列的前2008项和
(本小题满分12分) 
(1)求b的值
(2)求sinC的值
(本小题共12分)已知函数 .
.
(Ⅰ)求 的最小正周期;
的最小正周期;
(Ⅱ)求 在区间
在区间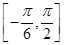 上的最大值和最小值.
上的最大值和最小值.
(本小题满分14分).如图,在三棱锥P-ABC中,PA⊥底面ABC,PA=AB,∠ABC=60°,∠BCA=90°,点D、E分别在棱PB、PC的中点,且DE∥BC.
(1)求证:DE∥平面ACD
(2)求证:BC⊥平面PAC;
(3)求AD与平面PAC所成的角的正弦值;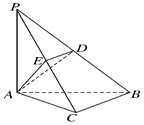
(本小题满分14分)
已知函数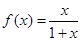
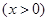 ,数列
,数列 满足:
满足: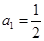 ,
,
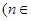 N*
N*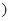 .
.
(1)求数列 的通项公式;
的通项公式;
(2)令函数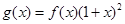 ,数列
,数列 满足:
满足: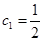 ,
, N*),
N*),
求证:对于一切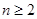 的正整数,都满足:
的正整数,都满足: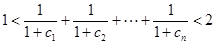 .
.
(本小题满分14分)
已知函数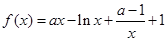 .
.
(1)当 时,求曲线
时,求曲线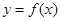 在点
在点 处的切线方程;
处的切线方程;
(2)当 时,讨论
时,讨论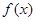 的单调性.
的单调性.