(本小题满分14分)已知数列 中,
中, ,其前
,其前 项和
项和 满足
满足 .
.
(Ⅰ)求证:数列 为等差数列,并求
为等差数列,并求 的通项公式;
的通项公式;
(Ⅱ)设 ,求数列
,求数列 的前
的前 项和
项和 ;
;
(Ⅲ)设 (
( 为非零整数,
为非零整数, ),是否存在确定
),是否存在确定 的值,使得对任意
的值,使得对任意 ,有
,有 恒成立.若存在求出
恒成立.若存在求出 的值,若不存在说明理由。
的值,若不存在说明理由。
已知数列 满足
满足
 是
是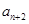 与
与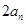 的等差中项
的等差中项
(1)证明:数列 是等比数列;
是等比数列;
(2)求数列 的通项公式;
的通项公式;
(本小题满分13分)已知函数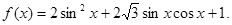 求:
求:
(1)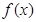 的最小正周期;(2)
的最小正周期;(2)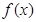 的单调递增区间;(3)
的单调递增区间;(3)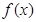 在
在 上的最值.
上的最值.
已知数列 是等比数列,首项
是等比数列,首项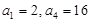
(Ⅰ)求数列 的通项公式(Ⅱ)若数列
的通项公式(Ⅱ)若数列 是等差数列,且
是等差数列,且 ,求数列
,求数列 的通项公式及前
的通项公式及前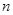 项的和
项的和
(本小题满分12分)四棱锥S-ABCD中,底面ABCD为平行四边形,侧面SBC⊥底面ABCD.已知∠ABC=45°,AB=2,BC=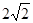 ,SA=SB=
,SA=SB= 。
。
(1)证明:SA⊥BC;
(2)求直线SD与平面SAB所成角的大小;
(3)求二面角D-SA-B的大小.
(本小题满分12分)如图,在四棱锥P-ABCD中,底面ABCD是边长为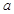 的正方形,E、F分别为PC、BD的中点,侧面PAD⊥底面ABCD,且PA=PD=
的正方形,E、F分别为PC、BD的中点,侧面PAD⊥底面ABCD,且PA=PD= AD.
AD.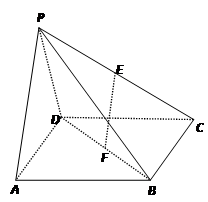
(1)求证:EF∥平面PAD;
(2)求证:平面PAB⊥平面PCD.