中国正在成为汽车生产大国,汽车保有量大增,交通拥堵日趋严重.某市有关部门进行了调研,相关数据显示,从上午 点到中午
点到中午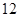 点,车辆通过该市某一路段的用时
点,车辆通过该市某一路段的用时 (分钟)与车辆进入该路段的时刻
(分钟)与车辆进入该路段的时刻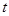 之间关系可近似地用如下函数给出:
之间关系可近似地用如下函数给出: ,
,
求从上午 点到中午
点到中午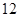 点,车辆通过该路段用时最多的时刻.
点,车辆通过该路段用时最多的时刻.
如图,在直三棱柱 中, AB=1,
中, AB=1, ,
,
∠ABC=60 .
.
(1)证明: ;
;
(2)求二面角A— —B的正切值。
—B的正切值。
已知复数
(1)设集合 中随机取一个数作为
中随机取一个数作为 ,从集合
,从集合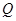 中随机取一个数
中随机取一个数
(2)设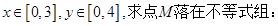
 所表示的平面区域内的概率。
所表示的平面区域内的概率。
已知向量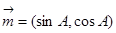 ,
,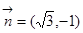 ,
,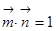 ,且
,且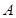 为锐角。
为锐角。
(1)求角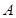 的大小;
的大小;
(2)求函数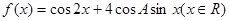 的值域。
的值域。
如图,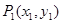 、
、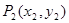 、…、
、…、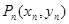
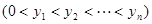 是曲线
是曲线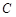 :
: 上的
上的 个点,点
个点,点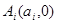 (
(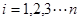 )在
)在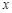 轴的正半轴上,且
轴的正半轴上,且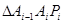 是正三角形(
是正三角形(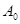 是坐标原点).
是坐标原点).
(1)写出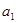 、
、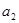 、
、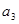 ;
;
(2)求出点 (
(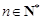 )的横坐标
)的横坐标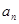 关于
关于 的表达式并证明.
的表达式并证明.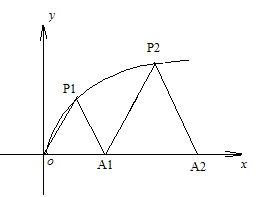
已知函数f(x)=x3-3x及y=f(x)上一点P(1,-2),过点P作直线l.
(1)求使直线l和y=f(x)相切且以P为切点的直线方程;
(2)求使直线l和y=f(x)相切且切点异于P的直线方程.