(本小题满分12分)设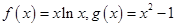 .
.
(1)令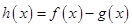 ,求
,求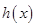 的单调区间;
的单调区间;
(2)若当 时,
时, 恒成立,求实数
恒成立,求实数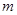 的取值范围;
的取值范围;
(本小题满分10分)在 中,角
中,角 所对的边分别为
所对的边分别为 、
、 、
、 ,且
,且 .(Ⅰ)求
.(Ⅰ)求 的值;(Ⅱ)若
的值;(Ⅱ)若 ,求
,求 的最大值.
的最大值.
(本小题满分12分)设函数
(1)当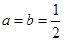 时,求函数
时,求函数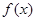 的最大值;
的最大值;
(2)令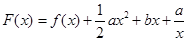 ,(
,( )其图象上任意一点
)其图象上任意一点 处切线的斜率
处切线的斜率 ≤
≤ 恒成立,求实数
恒成立,求实数 的取值范围;
的取值范围;
(3)当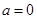 ,
, ,方程
,方程 有唯一实数解,求正数
有唯一实数解,求正数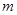 的值.
的值.
(本小题满分12分)已知椭圆 的左右焦点分别为
的左右焦点分别为 、
、 ,短轴两个端点为
,短轴两个端点为 、
、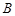 ,且四边形
,且四边形 是边长为2的正方形。
是边长为2的正方形。
(1)求椭圆方程;
(2)若 分别是椭圆长轴的左右端点,动点
分别是椭圆长轴的左右端点,动点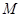 满足
满足 ,连接
,连接 ,交椭圆于点
,交椭圆于点 ;证明:
;证明: 为定值;
为定值;
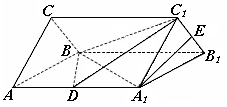
(本小题满分12分)如图,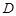 、
、 分别是正三棱柱
分别是正三棱柱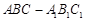 的棱
的棱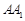 、
、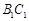 的中点,且棱
的中点,且棱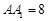 ,
,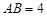 .
.
(Ⅰ)求证: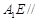 平面
平面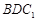 ;
;
(Ⅱ)在棱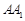 上是否存在一点
上是否存在一点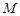 ,使二面角
,使二面角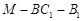 的大小为
的大小为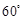 ,若存在,求
,若存在,求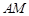 的长;若不存在,说明理由。
的长;若不存在,说明理由。
(本小题满分12分)在某学校组织的一次篮球定点投篮训练中,规定每人最多投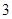 次:在
次:在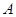 处每投进一球得
处每投进一球得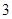 分,在
分,在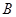 处每投进一球得
处每投进一球得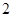 分;如果前两次得分之和超过
分;如果前两次得分之和超过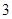 分即停止投篮,否则投第三次.某同学在
分即停止投篮,否则投第三次.某同学在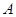 处的命中率
处的命中率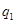 为
为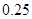 ,在
,在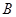 处的命中率为
处的命中率为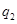 ,该同学选择先在
,该同学选择先在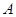 处投一球,以后都在
处投一球,以后都在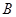 处投,用
处投,用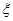 表示该同学投篮训练结束后所得的总分,其分布列为
表示该同学投篮训练结束后所得的总分,其分布列为
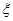 |
0 |
2 |
3 |
4 |
5 |
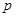 |
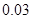 |
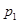 |
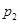 |
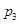 |
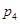 |
(1) 求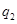 的值;
的值; (2) 求随机变量
(2) 求随机变量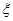 的数学期望
的数学期望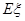 ;
;
(3) 试比较该同学选择都在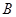 处投篮得分超过
处投篮得分超过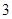 分与选择上述方式投篮得分超过
分与选择上述方式投篮得分超过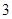 分的概率的大小.
分的概率的大小.