6盒火柴按“规则方式”打包,所谓“规则方式”是指每相邻2盒必须是以完全重合的面对接,最后得到的包装形式是一个长方体.已知火柴盒的长、宽、高尺寸分别是a=46mm,b=36mm,c=16mm,请你给出一种能使表面积最小的打包方式,并画出其示意图.
如图,A、B、C、D四点都在⊙O上,AD是⊙O的直径,且AD=6cm,若∠ABC= ∠CAD,求弦AC的长.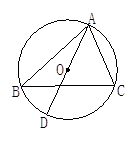
如图,AD为△ABC的外接圆O的直径,AE⊥BC于E,求证:∠BAD=∠EAC。
如图,圆柱形水管内原有积水的水平面宽CD=20cm,水深EB=2cm.求圆形的半径是多少。
某水果批发商场经销一种高档水果,如果每千克盈利10元,每天可售出500千克,经市场调查发现,在进货价不变的情况下,若每千克涨价1元,日销量减少20千克,现该商场要保证每天盈利6000元,同时又要使顾客得到实惠,那么每千克应涨价多少元?
某电脑公司2012年的各项经营收入中,经营电脑配件的收入为600万元,占全年经营总收入的40%,该公司预计2014年经营总收入要达到2160万元,且计划从2012年到2014年,每年经营总收入的年增长率相同,问每年的增长率是多少。