小王剪了两张直角三角形纸片,进行了如下的操作: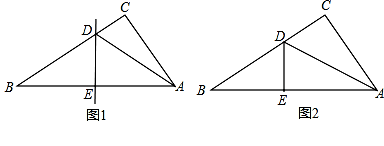
操作一:如图1,将Rt△ABC沿某条直线折叠,使斜边的两个端点A与B重合,折痕为DE.
(1)如果AC=6cm,BC=8cm,可求得△ACD的周长为 ;
(2)如果∠CAD:∠BAD=4:7,可求得∠B的度数为 ;
操作二:如图2,小王拿出另一张Rt△ABC纸片,将直角边AC沿直线AD折叠,使它落在斜边AB上,且与AE重合,若AC=9cm,BC=12cm,请求出CD的长.
在平面直角坐标系中,O为坐标原点,点A坐标为(1,0),以OA为边在第一象限内作等边△OAB,C为x轴正半轴上的一个动点(OC>1),连接BC,以BC为边在第一象限内作等边△BCD,直线DA交y轴于E点.
(1)如图,当C点在x轴上运动时,设AC=x,请用x表示线段AD的长;
(2)随着C点的变化,直线AE的位置变化吗?若变化,请说明理由;若不变,请求出直线AE的解析式.
(3)以线段BC为直径作圆,圆心为点F,
①当C点运动到何处时直线EF∥直线BO?此时⊙F和直线BO的位置关系如何?请说明理由.
②G为CD与⊙F的交点,H为直线DF上的一个动点,连结HG、HC,求HG+HC的最小值,并将此最小值用x表示.
如图1,Rt△ABC两直角边的边长为AC=3,BC=4.
(1)如图2,⊙O与Rt△ABC的边AB相切于点X,与边BC相切于点Y.请你在图2中作出并标明⊙O的圆心(用尺规作图,保留作图痕迹,不写作法和证明)
(2)P是这个Rt△ABC上和其内部的动点,以P为圆心的⊙P与Rt△ABC的两条边相切.设⊙P的面积为S,你认为能否确定S的最大值?若能,请你求出S的最大值;若不能,请你说明不能确定S的最大值的理由.
一家图文广告公司制作的宣传画板颇受商家欢迎,这种画板的厚度忽略不计,形状均为正方形,边长在10~30dm之间.每张画板的成本价(单位:元)与它的面积(单位:dm2)成正比例,每张画板的出售价(单位:元)由基础价和浮动价两部分组成,其中基础价与画板的大小无关,是固定不变的.浮动价与画板的边长成正比例.在营销过程中得到了表格中的数据.
| 画板的边长(dm) |
10 |
20 |
| 出售价(元/张) |
160 |
220 |
(1)求一张画板的出售价与边长之间满足的函数关系式;
(2)已知出售一张边长为30dm的画板,获得的利润为130元(利润=出售价-成本价),
①求一张画板的利润与边长之间满足的函数关系式;
②当边长为多少时,出售一张画板所获得的利润最大?最大利润是多少?
如图,AB是⊙O的直径,弦DE垂直平分半径OA,C为垂足,DE=3,连接DB,过点E作EM∥BD,交BA的延长线于点M.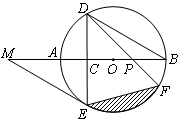
(1)求⊙O的半径;
(2)求证:EM是⊙O的切线;
(3)若弦DF与直径AB相交于点P,当∠APD=45º时,求图中阴影部分的面积.
抛物线y=ax2+2x+c与其对称轴相交于点A(1,4),与x轴正半轴交于点B.
(1)求这条抛物线的函数关系式;
(2)在抛物线对称轴上确定一点C,使△ABC是等腰三角形,求出所有点C的坐标.