（本题12分）如图，将透明三角形纸片PAB的直角顶点P落在第四象限，顶点A、B分别落在反比例函数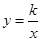
图像的两支上，且PB⊥x于点C，PA⊥y于点D，AB分别与x轴，y轴相交于点E、F，已知B（1，3）.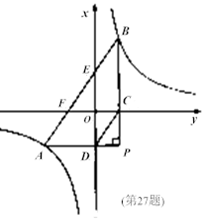
（1）k= ；
（2）试说明AE=BF;
（3）当四边形ABCD的面积为
时，求点P的坐标.
如图，AB、CD是半径为5的⊙O的两条弦，AB=8，CD=6，MN是直径，AB⊥MN于点E，CD⊥MN于点F，P为EF上的任意一点，则PA+PC的最小值为多少？
如图，在△ABC中，∠ABC=90°，AB=BC，BD为斜边AC上的中线，将△ABD绕点D顺时针旋转α（0°＜α＜180°），得到△EFD，点A的对应顶点是E，点B的对应顶点是F，连接BE、CF。试判断BE与CF的长度是否相等，并说明理由。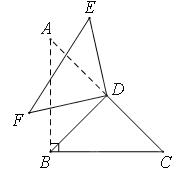
某校九年级学生进行校运会广播体操比赛，如果排成方阵（即正方形），则多出6人；如果每排减4人，排数多6，则缺2人。问该校九年级学生共有多少人？
有一道练习题：对于式子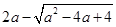
先化简，后求值，其中
。小明的解法如下：=
=
=
=
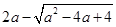。小明的解法对吗？如果不对，请帮他改正。
解方程：(1) x2=x (2) 