如图,矩形ABCD中,E为BC上一点,DF⊥AE于点F。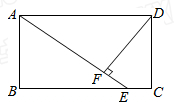
(1)求证:△ABE∽△DFA;
(2)若AB=6,AD=12,BE=8,求DF的长。
(11·丹东)(本题14分)已知:二次函数 与
与 轴交于A,B两点(点A在点B的左侧),点A、点B的横坐标是一元二次方程
轴交于A,B两点(点A在点B的左侧),点A、点B的横坐标是一元二次方程 的两个根.
的两个根.
(1)请直接写出点A、点B的坐标.
(2)请求出该二次函数表达式及对称轴和顶点坐标.
(3)如图1,在二次函数对称轴上是否存在点P,使 的周长最小,若存在
的周长最小,若存在 ,请求出点P的坐标;若不存在,请说明理由.
,请求出点P的坐标;若不存在,请说明理由.
(4)如图2,连接AC、BC,点Q是线段OB上一个动点(点Q不与点O、B重合). 过点Q作QD∥AC交于BC点D,设Q点坐标(m,0),当 面积S最大时,求m的值.
面积S最大时,求m的值.
(11·丹东)(本题10分)某食品加工厂需要一批食品包装盒,供应这种包装盒有两种方案可供选 择:
择:
方案一:从包装盒加工厂直接购买,购买所需的费用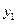 与包装盒数
与包装盒数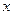 满足如图1所示的函数关系.
满足如图1所示的函数关系.
方案二:租赁机器自己加工,所需费用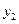 (包括租赁机器的费用和生产包装盒的费用)与包装盒
(包括租赁机器的费用和生产包装盒的费用)与包装盒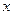 满足如图2所示的函数关系.
满足如图2所示的函数关系.
根据图像回答下列问题:
(1)方案一中每个包装盒的价格是多少元?
(2)方案二中租赁机器的费用是多少元?生产一个包装盒的费用是多少元 ?
?
(3)请分别求出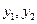 与
与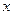 的函数关系式.
的函数关系式.
(4)如果你是决策者,你认为应该选择哪种方案更省钱?并说明理由.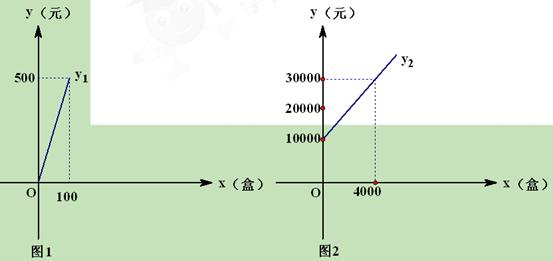
(11·丹东)(本题10分)某文具店老板第一次用1000元购进一批文具,很快销售完毕;第二次购进时发现每件文具进价比第一次上涨了2.5元.老板用2500元购进了第二批文具,所购进文具的数量是第一次购进数量的2倍,同样很快 销售完毕.两批文具的售价均为每件15元.
销售完毕.两批文具的售价均为每件15元.
(1)问第二次购进了多少件文具?
(2)文具店老板在这两笔生意中共盈利多少元?
(11·丹东)(本题10分)已知:如图,在 中,
中, ,以AC为直径作⊙O交AB于点D.
,以AC为直径作⊙O交AB于点D.
(1)若 ,求线段BD的长.
,求线段BD的长.
(2)若点E为线段BC的中点,连接DE.求证:DE是⊙O的切线.
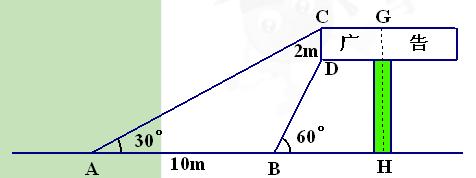
(11·丹东)(本题10分)数学兴趣小组想利用所学的知识了解某广告牌的高度,已知CD=2cm.经测量,得到其它数据如图所示.其中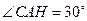 ,
,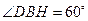 ,AB=10cm.请你根据以上数据计算GH的长.
,AB=10cm.请你根据以上数据计算GH的长.
(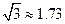 ,要求结果精确到0.1m)
,要求结果精确到0.1m)