已知函数 的最大值为
的最大值为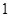 .
.
(Ⅰ)求常数 的值;
的值;
(Ⅱ)求函数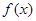 的单调递增区间;
的单调递增区间;
(Ⅲ)若将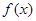 的图象向左平移
的图象向左平移 个单位,得到函数
个单位,得到函数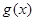 的图象,求函数
的图象,求函数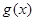 在区间
在区间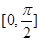 上的最大值和最小值.
上的最大值和最小值.
已知复数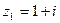 ,
,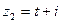 ,其中
,其中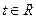 ,
,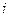 为虚数单位.
为虚数单位.
(1)若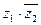 是实数(其中
是实数(其中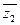 为
为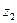 的共轭复数),求实数
的共轭复数),求实数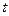 的值;
的值;
(2)若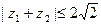 ,求实数
,求实数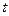 的取值范围.
的取值范围.
已知复数 ,其中
,其中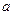 、
、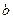 为实数,
为实数,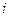 为虚数单位,
为虚数单位,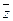 为
为 的共轭复数,且存在非零实数
的共轭复数,且存在非零实数 ,使
,使 成立.
成立.
(1)求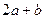 的值;
的值;
(2)若 ,求实数
,求实数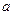 的取值范围.
的取值范围.
已知数列 的前
的前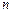 项和为
项和为 ,
, ,
, (
(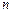 为正整数).
为正整数).
(1)求数列 的通项公式;
的通项公式;
(2)记 ,若对任意正整数
,若对任意正整数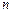 ,
, 恒成立,求
恒成立,求 的取值范围?
的取值范围?
(3)已知集合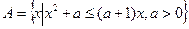 ,若以a为首项,a为公比的等比数列前n项和记为
,若以a为首项,a为公比的等比数列前n项和记为 ,问是否存在实数a使得对于任意的
,问是否存在实数a使得对于任意的 .若存在,求出a的取值范围;若不存在,说明理由.
.若存在,求出a的取值范围;若不存在,说明理由.
已知点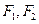 是双曲线M:
是双曲线M: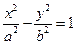 的左右焦点,其渐近线为
的左右焦点,其渐近线为 ,且右顶点到左焦点的距离为3.
,且右顶点到左焦点的距离为3.
(1)求双曲线M的方程;
(2) 过 的直线
的直线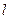 与M相交于
与M相交于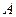 、
、 两点,直线
两点,直线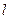 的法向量为
的法向量为 ,且
,且 ,求k的值;
,求k的值;
(3)在(2)的条件下,若双曲线M在第四象限的部分存在一点C满足 ,求m的值及△ABC的面积
,求m的值及△ABC的面积 .
.
已知函数 (k为常数),
(k为常数), 是函数
是函数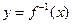 图像上的点.
图像上的点.
(1)求实数k的值及函数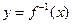 的解析式;
的解析式;
(2)将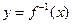 的图像按向量
的图像按向量 平移得到函数y=g(x)的图像.
平移得到函数y=g(x)的图像.
若 对任意的
对任意的 恒成立,试求实数m的取值范围.
恒成立,试求实数m的取值范围.