如图,在直三棱柱ABC﹣A1B1C1中,AB=2,AC=AA1=4,∠ABC=90°.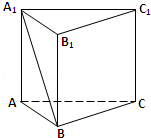
(1)求三棱柱ABC﹣A1B1C1的表面积S;
(2)求异面直线A1B与AC所成角的余弦值.
已知关于x的不等式|ax-1|+|ax-a|≥2(a>0).
(1)当a=1时,求此不等式的解集;
(2)若此不等式的解集为R,求实数a的取值范围.
设函数f(x)=|x-a|+3x,其中a>0.
(1)当a=1时,求不等式f(x)≥3x+2的解集;
(2)若不等式f(x)≤0的解集为{x|x≤-1},求a的值.
已知函数f(x)=|x-a|.
(1)若不等式f(x)≤3的解集为{x|-1≤x≤5},求实数a的值;
(2)在(1)的条件下,若f(x)+f(x+5)≥m对一切实数x恒成立,求实数m的取值范围.
已知函数f(x)=|x-1|+|x-2|.若不等式|a+b|+|a-b|≥|a|f(x)(a≠0,a、b∈R)恒成立,求实数x的取值范围.
解不等式|2x-4|<4-|x|.