在平面直角坐标系中，O为坐标原点，点A坐标为（1，0），以OA为边在第一象限内作等边△OAB，C为x轴正半轴上的一个动点（OC＞1），连接BC，以BC为边在第一象限内作等边△BCD，直线DA交y轴于E点．
（1）如图，当C点在x轴上运动时，设AC＝x，请用x表示线段AD的长；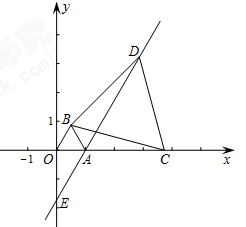
（2）随着C点的变化，直线AE的位置变化吗？若变化，请说明理由；若不变，请求出直线AE的解析式．
（3）以线段BC为直径作圆，圆心为点F，当C点运动到何处时直线EF∥直线BO？此时⊙F和直线BO的位置关系如何？请说明理由．
（4）G为CD与⊙F的交点，H为直线DF上的一个动点，连结HG、HC，求HG＋HC的最小值，并将此最小值用x表示．
QQ农场是同学们非常熟悉的一款游戏，其升级经验值增加规则为：下一级的升级经验比上一级多200分，可用如下的代数式表示：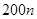
点（其中
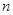为下一等级）.
下图是一网民的QQ农场的截图，根据图中的经验值计算该网民QQ农场现在的等级
为多少级？（2948表示目前的经验值，10000表示下一级需要的经验值）如果该网民想升级到60级，那么从一开始（0级）累计需要的经验值为多少点？
如图，大正方形是由两个小正方形和两个长方形拼成的.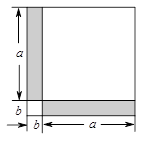
请你用两个不同形式的代数式表示这个大正方形的面积
由（1）可得到关于
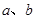的等式，利用得到的这个等式计算：
4.3232+2×4.323×0.677+0.6772.
已知多项式
，计算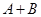
．某同学做此题时误将
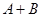看成了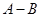
，求得其结果为
=
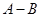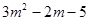，若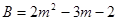
，请你帮助他求得正确答案．
在某次抗险救灾中，消防官兵的冲锋舟沿东西方向的河流抢救灾民，早晨从A地出发，晚上到达B 地，约定向东为正方向，当天的航行路程记录如下（单位：千米）：+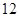
，
， 
，
，+
，
，
，
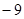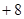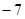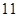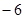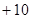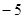
B地在A地何处？
若冲锋舟每千米耗油0. 5升，油箱容量为30升，求途中还需补充多少升油？
人在运动时的心跳速率通常与人的年龄有关，如果用
表示一个人的年龄，用
表示正常情况下的这个人在运动时所能承受的每分钟心跳的最高次数，那么
.正常情况下，在运动时，一个16岁的少年所能承受的每分钟心跳的最高次数是多少？
一个50岁的人运动时，30秒心跳的次数为70次，他有危险吗？