有一种可食用的野生菌，刚上市时，外商李经理以每千克30元的市-优题课

有一种可食用的野生菌，刚上市时，外商李经理以每千克30元的市场价格收购了这种野生菌1000千克存放入冷库中，据预测，该野生菌的市场价格将每天每千克上涨1元；但冷冻存放这批野生菌时每天需要支出各种费用合计310元，而且这种野生菌在冷库中最多保存140天，同时，平均每天有3千克的野生菌损坏导致不能出售．
（1）若存放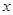天后，将这批野生菌一次性出售，设这批野生菌的销售总额为元，试求出与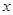之间的函数关系式；
（2）李经理将这批野生菌存放多少天后一次性全部出售可以获得22500元的利润？

科目数学题型解答题难度中等

知识点：二次函数在给定区间上的最值

某商店销售一种销售成本为每件40元的玩具，若按每件50元销售，一个月可售出500件，销售价每涨1元，月销量就减少10件．设销售价为每件 $x$ 元 $(x ⩾ 50)$ ，月销量为 $y$ 件，月销售利润为 $w$ 元．

（1）写出 $y$ 与 $x$ 的函数解析式和 $w$ 与 $x$ 的函数解析式；

（2）商店要在月销售成本不超过10000的情况下，使月销售利润达到8000元，销售价应定为每件多少元？

（3）当销售价定为每件多少元时会获得最大利润？求出最大利润．

如图， $⊙ O$ 是 $ΔABC$ 的外接圆，直线 $EG$ 与 $⊙ O$ 相切于点 $E$ ， $EG / / BC$ ，连接 $AE$ 交 $BC$ 于点 $D$ ．

（1）求证： $AE$ 平分 $∠ BAC$ ；

（2）若 $∠ ABC$ 的平分线 $BF$ 交 $AD$ 于点 $F$ ，且 $DE = 3$ ， $DF = 2$ ，求 $AF$ 的长．

某校为了了解初中学生每天的睡眠时间（单位为小时），随机调查了该校的部分初中学生，根据调查结果，绘制出如图统计图．

请根据相关信息，解答下列问题：

（1）本次接受调查的初中学生人数为　　人，扇形统计图中的 $m =$ 　　，条形统计图中的 $n =$ 　　；

（2）所调查的初中学生每天睡眠时间的众数是　　，方差是　　；

（3）该校共有1600名初中学生，根据样本数据，估计该校初中学生每天睡眠时间不足8小时的人数．

已知：如图，在正方形 $ABCD$ 中，对角线 $AC$ ， $BD$ 相交于点 $O$ ，点 $E$ ， $F$ 分别是边 $BC$ ， $CD$ 上的点，且 $∠ EOF = 90 °$ ．

求证： $CE = DF$ ．

一个不透明的口袋中装有三个完全相同的小球，上面分别标有数字 $\sqrt{2}$ ， $\sqrt{3}$ ，5．

（1）从口袋中随机摸出一个小球，求摸出小球上的数字是无理数的概率（直接写出结果）；

（2）先从口袋中随机摸出一个小球，将小球上的数字记为 $x$ ，把小球放回口袋中并搅匀，再从口袋中随机摸出一个小球，将小球上的数字记为 $y$ ．请用列表法或画树状图法求出 $x$ 与 $y$ 的乘积是有理数的概率．

试卷网试题网古诗词网作文网范文网