设
(本小题满分12分)
为支持2 010年广洲亚运会,某班拟选派4人为志愿者参与亚运会,经过初选确定5男4女共9名同学成为候选人,每位候选人当选志愿者的机会均等。
010年广洲亚运会,某班拟选派4人为志愿者参与亚运会,经过初选确定5男4女共9名同学成为候选人,每位候选人当选志愿者的机会均等。
(1)求女生1人,男生3人当选时的概率?
(2)设至少有几名男同学当选的概率为 ,当
,当 时,n的最小值?
时,n的最小值?
(本小题满分10分)
在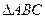 中,
中, 、
、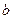 、
、 分别为角A、B、C的对边,且
分别为角A、B、C的对边,且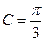 ,
, ,(其中
,(其中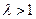 ).
). (Ⅰ)若
(Ⅰ)若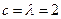 时,求
时,求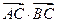 的值;
的值;
(Ⅱ)若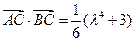 时,求边长
时,求边长 的最小值及判定此时
的最小值及判定此时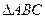 的形状。
的形状。
选修4—5:不等式选讲
已知函数
(1)解关于 的不等式
的不等式 ;
;
(2)若函数 的图象恒在函数
的图象恒在函数 图象的上方,求
图象的上方,求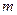 的取值范围。
的取值范围。
选修4—4:坐标系与参数方程
以直角坐标系的原点 为极点,
为极点, 轴的正半轴为极轴,已知点
轴的正半轴为极轴,已知点 的直角坐标为
的直角坐标为 ,点
,点 的极坐标为
的极坐标为 ,若直线
,若直线 过点
过点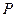 ,且倾斜角为
,且倾斜角为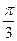 ,圆
,圆 以
以 为 圆心、
为 圆心、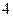 为半径。
为半径。
(1)求直线 的参数方程和圆
的参数方程和圆 的极坐标方程;
的极坐标方程;
(2)试判定直线 和圆
和圆 的位置关系。
的位置关系。
(选修4—1:平面几何
如图,Δ
 是内接于⊙O,
是内接于⊙O, ,
,
直线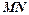 切⊙O于点
切⊙O于点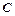 ,弦
,弦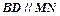 ,
,
与 相交于点
相交于点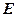 .
.
(1)求证:Δ ≌Δ
≌Δ ;
;
(2)若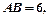
 ,求
,求 .
.