(本小题满分12分)
为支持2 010年广洲亚运会,某班拟选派4人为志愿者参与亚运会,经过初选确定5男4女共9名同学成为候选人,每位候选人当选志愿者的机会均等。
010年广洲亚运会,某班拟选派4人为志愿者参与亚运会,经过初选确定5男4女共9名同学成为候选人,每位候选人当选志愿者的机会均等。
(1)求女生1人,男生3人当选时的概率?
(2)设至少有几名男同学当选的概率为 ,当
,当 时,n的最小值?
时,n的最小值?
在回归分析中,通过模型由解释变量计算预报变量的值时,应注意什么问题?
在空间直角坐标系中,已知A(3,0,1)和B(1,0,﹣3),试问
(1)在y轴上是否存在点M,满足|MA|=|MB|?
(2)在y轴上是否存在点M,使△MAB为等边三角形?若存在,试求出点M坐标.
如图,已知正方体ABCD﹣A′B′C′D′的棱长为a,M为BD′的中点,点N在A′C′上,且|A′N|=3|NC′|,试求MN的长.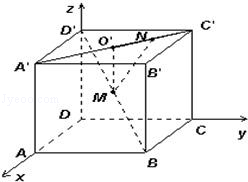
已知A(1,﹣2,11),B(4,2,3),C(6,﹣1,4),求证其为直角三角形.
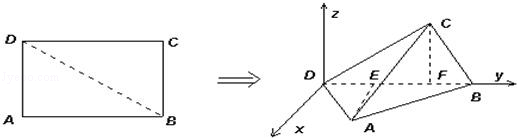
如图,已知矩形ABCD中,|AD|=3,|AB|=4.将矩形ABCD沿对角线BD折起,使得面BCD⊥面ABD.现以D为原点,DB作为y轴的正方向,建立如图空间直角坐标系,此时点A恰好在xDy坐标平面内.试求A,C两点的坐标.