同时抛掷两颗骰子，求：
(1)点数之和是4的倍数的概率；
(2)点数之和大于5小于10的概率；
(3)点数之和大于3的概率．
已知圆C的方程为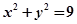
，点A
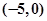，直线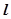
：
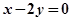
（1）求与圆C相切，且与直线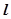垂直的直线方程；
（2）O为坐标原点，在直线OA上是否存在异于A点的B点，使得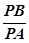
为常数，若存在，求出点B，不存在说明理由.
已知圆C1：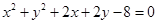
与圆C2：
相交于A、B两点，
(1)求公共弦AB所在的直线方程；
(2)求圆心在直线
上，且经过A、B两点的圆的方程．
已知圆 C方程为
.
（1）若圆C与直线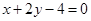
相交于M、N两点，且OM⊥ON（O为坐标原点），求m；
（2）在（1）的条件下，求以MN为直径的圆的方程.
已知圆C与圆
相外切，并且与直线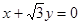
相切于点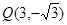
，求圆C的
中，已知
，且对任意
，总有
成等差数列，其公差为
．
，
，
成等比数列；
，证明：
．