某重点大学自主招生考试过程依次为自荐材料审查、笔试、面试共三轮考核。规定:只能通过前一轮考核才能进入下一轮的考核,否则将被淘汰;三轮考核都通过才算通过该高校的自主招生考试。学生甲三轮考试通过的概率分别为 ,
, ,
, ,且各轮考核通过与否相互独立。
,且各轮考核通过与否相互独立。
(1)求甲通过该高校自主招生考试的概率;
(2)若学生甲每通过一轮考核,则家长奖励人民币1000元作为大学学习的教育基金。记学生甲得到教育基金的金额为 ,求
,求 的分布列和数学期望。
的分布列和数学期望。
(本小题满分14分)已知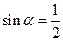 , (1)求角
, (1)求角 所在象限;(2)求
所在象限;(2)求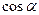 及
及 的值。
的值。
已知函数 ,
,
(1)求函数的定义域及值域;
(2)判断该函数的奇偶性,并证明你的结论.
(本小题满分14分)已知圆C: ,
,
(1)求出此圆圆心C的坐标和半径r;
(2)求直线y=x被圆C所截得的弦长.
(本小题满分14分)已知x,y之间的一组数据如下表:
| x |
1 |
3 |
6 |
7 |
8 |
| y |
1 |
2 |
3 |
4 |
5 |
(1)以x为横坐标,y为纵坐标在直角坐标系中画出散点图,并说明这两个变量之间的关系是正相关关系还是负相关关系。
(2)求线性回归方程.
(本小题满分14分)为了检测某条生产线上产品的尺寸。现从该条生产线上每隔一定时间取一件产品,共取了50件,测得其产品尺寸后,画得其频率分布直方图如下。
|

 内产品的个数.
内产品的个数.