设函数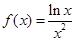 ,
,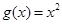 .
.
(1)求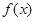 的极大值;
的极大值;
(2)求证:
(3)当方程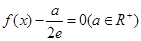 有唯一解时,试探究函数
有唯一解时,试探究函数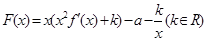 与
与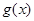 的图象在其公共点处是否存在公切线,若存在.研究
的图象在其公共点处是否存在公切线,若存在.研究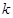 的值的个数;若不存在,请说明理由.
的值的个数;若不存在,请说明理由.
已知数列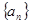 中
中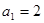 ,点
,点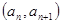 在函数
在函数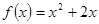 的图象上,
的图象上,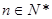 .数列
.数列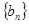 的前
的前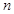 项和为
项和为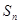 ,且满足
,且满足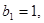 当
当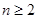 时,
时,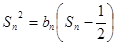
(1)证明数列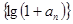 是等比数列;
是等比数列;
(2)求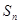 ;
;
(3)设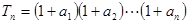 ,
,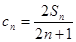 ,求
,求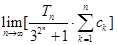 的值.
的值.
已知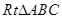 两锐角
两锐角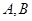 的正弦值,是实系数方程
的正弦值,是实系数方程 的两根.若
的两根.若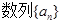 满足
满足 且
且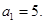 试求数列
试求数列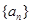
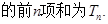
甲有一只放有a本《周易》,b本《万年历》,c本《吴从纪要》的书箱,且a+b+c ="6" (a,b,c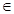 N),乙也有一只放有3本《周易》,2本《万年历》,1《吴从纪要》的书箱,两人各自从自己的箱子中任取一本书(由于每本书厚薄、大小相近,每本书被抽取出的可能性一样),规定:当两本书同名时甲将被派出去完成某项任务,否则乙去.
N),乙也有一只放有3本《周易》,2本《万年历》,1《吴从纪要》的书箱,两人各自从自己的箱子中任取一本书(由于每本书厚薄、大小相近,每本书被抽取出的可能性一样),规定:当两本书同名时甲将被派出去完成某项任务,否则乙去.
(1) 用a、b、c表示甲去的概率;
(2) 若又规定:当甲取《周易》,《万年历》,《吴从纪要》而去的得分分别为1分、2分、3分,否则得0分,求甲得分的期望的最大值及此时a、b、c的值.
设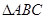 的内角
的内角 所对的边分别为
所对的边分别为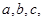 且
且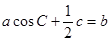 .
.
(1)求角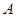 的大小;
的大小;
(2)若 ,求
,求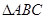 的周长
的周长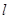 的取值范围.
的取值范围.
设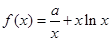 ,
, .
.
(1)当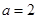 时,求曲线
时,求曲线 在
在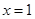 处的切线方程;
处的切线方程;
(2)如果存在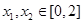 ,使得
,使得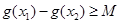 成立,求满足上述条件的最大整数
成立,求满足上述条件的最大整数 ;
;
(3)如果对任意的 ,都有
,都有 成立,求实数
成立,求实数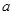 的取值范围
的取值范围