(本题12分)某校从参加某次知识竞赛的同学中,选取60名同学将其成绩(百分制)(均为整数)分成6组后,得到部分频率分布直方图(如图),观察图形中的信息,回答下列问题.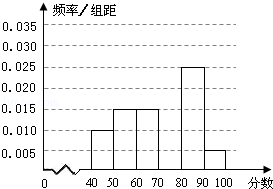
(1)求分数在[70,80)内的频率,并补全这个频率分布直方图;
(2)从频率分布直方图中,估计本次考试的平均分;
(3)若从60名学生中随机抽取2人,抽到的学生成绩在[40,70)记0分,在[70,100]记1分,用X表示抽取结束后的总记分,求X的分布列和数学期望.
(理)正数列 的前
的前 项和
项和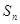 满足:
满足: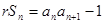 ,
,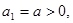 常数
常数
(1)求证: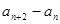 是一个定值;
是一个定值;
(2)若数列 是一个周期数列,求该数列的周期;
是一个周期数列,求该数列的周期;
(3)若数列 是一个有理数等差数列,求
是一个有理数等差数列,求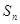 .
.
、出租车几何学是由十九世纪的赫尔曼-闵可夫斯基所创立的。在出租车几何学中,点还是形如 的有序实数对,直线还是满足
的有序实数对,直线还是满足 的所有
的所有 组成的图形,角度大小的定义也和原来一样。直角坐标系内任意两点
组成的图形,角度大小的定义也和原来一样。直角坐标系内任意两点 定义它们之间的一种“距离”:
定义它们之间的一种“距离”: ,请解决以下问题:
,请解决以下问题:
1、(理)求线段
 上一点
上一点 的距离到原点
的距离到原点 的“距离”;
的“距离”;
(文)求点 、
、 的“距离”
的“距离” ;
;
2、(理)定义:“圆”是所有到定点“距离”为定值的点组成的图形,
求“圆周”上的所有点到点 的“距离”均为
的“距离”均为  的“圆”方程;
的“圆”方程;
(文)求线段
 上一点
上一点 的距离到原点
的距离到原点 的“距离”;
的“距离”;
3、(理)点 、
、 ,写出线段
,写出线段 的垂直平分线的轨迹方程并画出大致图像.
的垂直平分线的轨迹方程并画出大致图像.
(文)定义:“圆”是所有到定点“距离”为定值的点组成的图形,点 、
、 ,
, ,求经过这三个点确定的一个“圆”的方程,并画出大致图像;
,求经过这三个点确定的一个“圆”的方程,并画出大致图像;
(说明所给图形小正方形的单位是1)
(文)函数 ,
,
定义 的第
的第 阶阶梯函数
阶阶梯函数 ,其中
,其中 ,
, 的各阶梯函数图像的最高点
的各阶梯函数图像的最高点 ,
,
(1)直接写出不等式 的解;
的解;
(2)求证:所有的点 在某条直线
在某条直线 上.
上.
(理)函数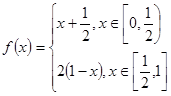 ,
,
定义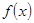 的第
的第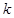 阶阶梯函数
阶阶梯函数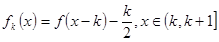 ,其中
,其中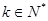 ,
,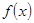 的各阶梯函数图像的最高点
的各阶梯函数图像的最高点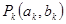 ,最低点
,最低点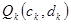
(1)直接写出不等式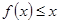 的解;
的解;
(2)求证:所有的点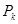 在某条直线
在某条直线 上.
上.
(3)求证:点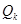 到(2)中的直线
到(2)中的直线 的距离是一个定值.
的距离是一个定值.
已知直角坐标平面内点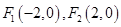 ,一曲线
,一曲线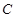 经过点
经过点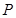 ,且
,且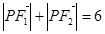
(1)求曲线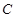 的方程;
的方程;
(2)设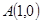 ,若
,若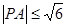 ,求点
,求点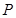 的横坐标的取值范围.
的横坐标的取值范围.