(本小题满分8分)
已知全集 ,
,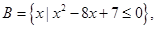
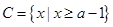
(1)求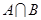 ;
; 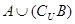
(2)若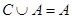 ,求实数
,求实数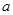 的取值范围.
的取值范围.
某休闲场馆举行圣诞酬宾活动,每位会员交会员费50元,可享受20元的消费,并参加一次抽奖活动,从一个装有标号分别为1,2,3,4,5,6的6只均匀小球的抽奖箱中,有放回的抽两次球,抽得的两球标号之和为12,则获一等奖价值a元的礼品,标号之和为11或10,获二等奖价值100元的礼品,标号之和小于10不得奖.
(1)求各会员获奖的概率;
(2)设场馆收益为ξ元,求ξ的分布列;假如场馆打算不赔钱,a最多可设为多少元?
已知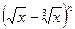 的二项展开式中所有奇数项的系数之和为512,
的二项展开式中所有奇数项的系数之和为512,
(1)求展开式的所有有理项(指数为整数).
(2)求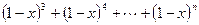 展开式中
展开式中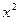 项的系数.
项的系数.
已知甲、乙、丙三名射击运动员集中目标的概率分别是0.7,0.8,0.85,若他们分别向目标各发一枪,命中弹数记为X,求X的分布列及期望.
有4个不同的球,四个不同的盒子,把球全部放入盒内.
(1)共有多少种放法?
(2)恰有一个盒内放2个球,有多少种放法?
有20件产品,其中5件是次品,其余都是合格品,现不放回的从中依次抽2件.
求:⑴第一次抽到次品的概率;
⑵第一次和第二次都抽到次品的概率;