已知在纸面上有一数轴(如图),折叠纸面.(1)若表示数1的点与表示数-1的点重合,则表示-2的点与表示数 的点重合;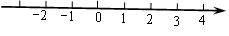
(2)若表示数-1的点与表示数3的点重合,回答以下问题:
① 表示数5的点与表示数 的点重合;
②若数轴上A、B两点之间的距离为9(A在B的左侧),且A、B两点经折叠后重合,求A、B两点表示的数是多少?
化简:(1+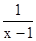 )÷
)÷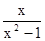 .
.
计算: -
- .
.
如图,在直角坐标系中,矩形 的顶点
的顶点 与坐标原点重合,顶点
与坐标原点重合,顶点 在坐标轴上,
在坐标轴上, ,
, .动点
.动点 从点
从点 出发,以
出发,以 的速度沿
的速度沿 轴匀速向点
轴匀速向点 运动,到达点
运动,到达点 即停止.设点
即停止.设点 运动的时间为
运动的时间为 .
.
(1)过点 作对角线
作对角线 的垂线,垂足为点
的垂线,垂足为点 .求
.求 的长
的长 与时间
与时间 的函数关系式,并写出自变量
的函数关系式,并写出自变量 的取值范围;
的取值范围;
(2)在点 运动过程中,当点
运动过程中,当点 关于直线
关于直线 的对称点
的对称点 恰好落在对角线
恰好落在对角线 上时,求此时直线
上时,求此时直线 的函数解析式;
的函数解析式;
(3)探索:以 三点为顶点的
三点为顶点的 的面积能否达到矩形
的面积能否达到矩形 面积的
面积的 ?请说明理由.
?请说明理由.
如图1,点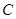 将线段
将线段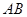 分成两部分,如果
分成两部分,如果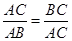 ,那么称点
,那么称点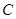 为线段
为线段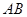 的黄金分割点.
的黄金分割点.
某研究小组在进行课题学习时,由黄金分割点联想到“黄金分割线”,类似地给出“黄金分割线”的定义:直线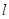 将一个面积为
将一个面积为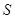 的图形分成两部分,这两部分的面积分别为
的图形分成两部分,这两部分的面积分别为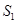 ,
,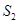 ,如果
,如果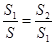 ,那么称直线
,那么称直线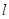 为该图形的黄金分割线.
为该图形的黄金分割线.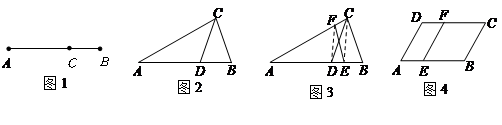
(1)研究小组猜想:在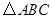 中,若点
中,若点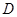 为
为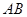 边上的黄金分割点(如图2),则直线
边上的黄金分割点(如图2),则直线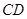 是
是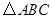 的黄金分割线.你认为对吗?为什么?
的黄金分割线.你认为对吗?为什么?
(2)请你说明:三角形的中线是否也是该三角形的黄金分割线?
(3)研究小组在进一步探究中发现:过点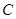 任作一条直线交
任作一条直线交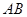 于点
于点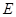 ,再过点
,再过点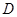 作直线
作直线 ,交
,交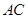 于点
于点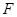 ,连接
,连接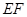 (如图3),则直线
(如图3),则直线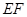 也是
也是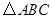 的黄金分割线.
的黄金分割线.
请你说明理由.
(4)如图4,点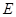 是
是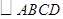 的边
的边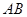 的黄金分割点,过点
的黄金分割点,过点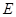 作
作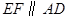 ,交
,交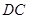 于点
于点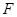 ,显然直线
,显然直线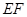 是
是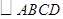 的黄金分割线.请你画一条
的黄金分割线.请你画一条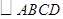 的黄金分割线,使它不经过
的黄金分割线,使它不经过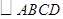 各边黄金分割点.
各边黄金分割点.
某地区一种商品的需求量
(万件)、供应量
(万件)与价格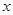 (元/件)分别近似满足下列函数关系式:
,
.需求量为0时,即停止供应.当
时,该商品的价格称为稳定价格,需求量称为稳定需求量.
(元/件)分别近似满足下列函数关系式:
,
.需求量为0时,即停止供应.当
时,该商品的价格称为稳定价格,需求量称为稳定需求量.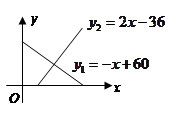
(1)求该商品的稳定价格与稳定需求量;
(2)价格在什么范围,该商品的需求量低于供应量?
(3)当需求量高于供应量时,政府常通过对供应方提供价格补贴来提高供货价格,以提高供应量.现若要使稳定需求量增加4万件,政府应对每件商品提供多少元补贴,才能使供应量等于需求量?