甲、乙两个小组各10名同学进行英语口语会话练习,各练习5次,他们每个同学合格的次数分别如下:甲组:4,1,2,2,1,3,3,1,2,1.
乙组:4,3,0,2,1,3,3,0,1,3.
(1)如果合格3次以上(含3次)作为及格标准,请你说明哪个小组的及格率高?
(2)试计算两个小组的方差,请你比较哪个小组的口语会话的合格次数比较稳定?
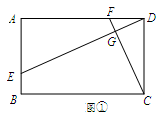
已知四边形ABCD中,E、F分别是AB、AD边上的点,DE与CF交于点G.
(1)如图①,若四边形ABCD是矩形,且DE⊥CF,求证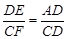 ;
; 
(2)如图②,若四边形ABCD是平行四边形,试探究:当∠B与∠EGC满足什么关系时,使得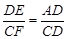 成立?并证明你的结论;
成立?并证明你的结论; 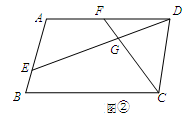
(3)如图③,若BA=BC=6,DA=DC=8,∠BAD=90°,DE⊥CF,请直接写出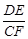 的值.
的值.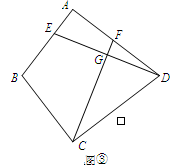
科幻小说《实验室的故事》中,有这样一个情节,科学家把一种珍奇的植物分别放在不同温度的环境中,经过一天后,测试出这种植物高度的增长情况(如下表):
温度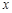 /℃ /℃ |
…… |
-4 |
-2 |
0 |
2 |
4 |
4.5 |
…… |
植物每天高度增长量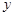 /mm /mm |
…… |
41 |
49 |
49 |
41 |
25 |
19.75 |
…… |
由这些数据,科学家推测出植物每天高度增长量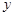 是温度
是温度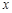 的函数,且这种函数是反比例函数、一次函数和二次函数中的一种.
的函数,且这种函数是反比例函数、一次函数和二次函数中的一种.
(1)请你选择一种适当的函数,求出它的函数关系式,并简要说明不选择另外两种函数的理由;
(2)温度为多少时,这种植物每天高度的增长量最大?
(3)如果实验室温度保持不变,在10天内要使该植物高度增长量的总和超过250mm,那么实验室的温度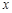 应该在哪个范围内选择?请直接写出结果.
应该在哪个范围内选择?请直接写出结果.
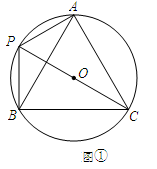
如图,在平面直角坐标系中,△ABC是⊙O的内接三角形,AB=AC,点P是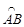 的中点,连接PA,PB,PC.
的中点,连接PA,PB,PC.
(1)如图①,若∠BPC=60°,求证: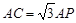 ;
;
(2)如图②,若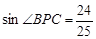 ,求
,求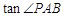 的值.
的值.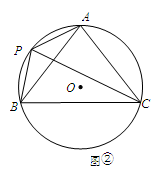
如图,在平面直角坐标系中,Rt△ABC的三个顶点分别是A(-3,2),B(0,4),C(0,2).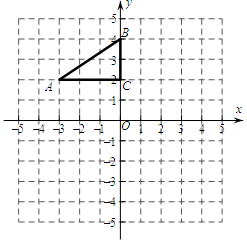
(1)将△ABC以点C为旋转中心旋转180°,画出旋转后对应的△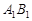 C;平移△ABC,若A的对应点
C;平移△ABC,若A的对应点 的坐标为(0,4),画出平移后对应的△
的坐标为(0,4),画出平移后对应的△ ;
;
(2)若将△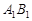 C绕某一点旋转可以得到△
C绕某一点旋转可以得到△ ,请直接写出旋转中心的坐标;
,请直接写出旋转中心的坐标;
(3)在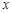 轴上有一点P,使得PA+PB的值最小,请直接写出点P的坐标.
轴上有一点P,使得PA+PB的值最小,请直接写出点P的坐标.
有两把不同的锁和四把不同的钥匙,其中两把钥匙恰好分别能打开这两把锁,其余的钥匙不能打开这两把锁.现在任意取出一把钥匙去开任意一把锁.
(1)请用列表或画树状图的方法表示出上述试验所有可能结果;
(2)求一次打开锁的概率.