已知四边形ABCD顶点都在4×4的正方形网格格点上,如图所示,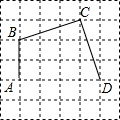
(1)请画出四边形ABCD的外接圆,并标明圆心M的位置;
(2)这个圆中弦BC所对的圆周角的度数是 。
如图,B、C、E三点在同一条直线上,AC∥DE,AC=CE,∠ACD=∠B. (1)求证:△ABC≌△CDE;
(1)求证:△ABC≌△CDE;
(2)若∠A=40°求∠BCD的度数.
已知方程组 的解适
的解适 合x+y=2,求m的值.
合x+y=2,求m的值.
解方程组:
分解因式:
(1) m2+4m+4
(2) a2b-4ab2+3b3
(3)(x2+y2)2-4x2y2
如图(十一)所示,在平面直角坐标系Oxy中,已知点A(-,0),点C(0,3),点B是x轴上一点(位于点A的右侧),以AB为直径的圆恰好经过点C.
(1)求∠ACB的度数;
(2)已知抛物线y=ax2+bx+3经过A、B两点,求抛物线的解析式;
(3)线段BC上是否存在点D,使△BOD为等腰三角形.若存在,则求出所有 符合条件的点D的坐标;若不存在,请说明理由.
符合条件的点D的坐标;若不存在,请说明理由.