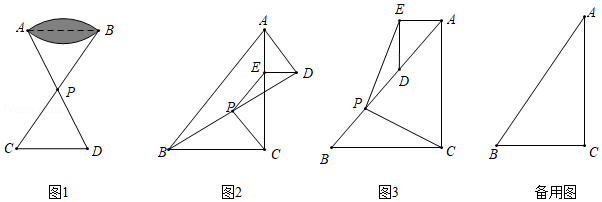
如图,B、C、E三点在同一条直线上,AC∥DE,AC=CE,∠ACD=∠B. (1)求证:△ABC≌△CDE;
(1)求证:△ABC≌△CDE;
(2)若∠A=40°求∠BCD的度数.
(1)阅读材料:
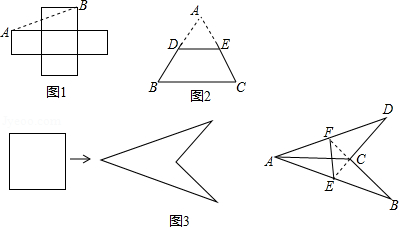
教材中的问题,如图1,把5个边长为1的小正方形组成的十字形纸板剪开,使剪成的若干块能够拼成一个大正方形,小明的思考:因为剪拼前后的图形面积相等,且5个小正方形的总面积为5,所以拼成的大正方形边长为 ,故沿虚线 剪开可拼成大正方形的一边,请在图1中用虚线补全剪拼示意图.
(2)类比解决:
如图2,已知边长为2的正三角形纸板 ,沿中位线 剪掉 ,请把纸板剩下的部分 剪开,使剪成的若干块能够拼成一个新的正三角形.
①拼成的正三角形边长为 ;
②在图2中用虚线画出一种剪拼示意图.
(3)灵活运用:
如图3,把一边长为 的正方形彩纸剪开,用剪成的若干块拼成一个轴对称的风筝,其中 ,延长 、 分别与 、 交于点 、 ,点 、 分别为 、 的中点,在线段 和 处用轻质钢丝做成十字形风筝龙骨,在图3的正方形中画出一种剪拼示意图,并求出相应轻质钢丝的总长度.(说明:题中的拼接都是不重叠无缝隙无剩余)
一只不透明的袋子中装有1个红球、1个黄球和1个白球,这些球除颜色外都相同
(1)搅匀后从袋子中任意摸出1个球,求摸到红球的概率;
(2)搅匀后从袋子中任意摸出1个球,记录颜色后放回、搅匀,再从中任意摸出1个球,求两次都摸到红球的概率.
为了解某市市民晚饭后1小时内的生活方式,调查小组设计了“阅读”、“锻炼”、“看电视”和“其它”四个选项,用随机抽样的方法调查了该市部分市民,并根据调查结果绘制成如下统计图.
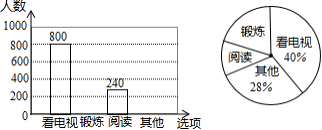
根据统计图所提供的信息,解答下列问题:
(1)本次共调查了 名市民;
(2)补全条形统计图;
(3)该市共有480万市民,估计该市市民晚饭后1小时内锻炼的人数.
如图,在平面直角坐标系中,抛物线 与 轴交于 , 两点(点 在点 的左侧),与 轴交于点 ,抛物线经过点 和点 ,点 是第一象限抛物线上的一个动点.
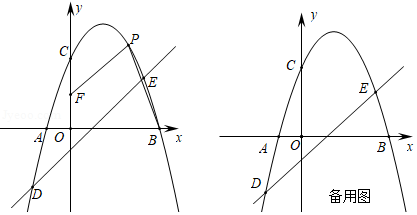
(1)求直线 和抛物线的表达式;
(2)在 轴上取点 ,连接 , ,当四边形 的面积是7时,求点 的坐标;
(3)在(2)的条件下,当点 在抛物线对称轴的右侧时,直线 上存在两点 , (点 在点 的上方),且 ,动点 从点 出发,沿 的路线运动到终点 ,当点 的运动路程最短时,请直接写出此时点 的坐标.
思维启迪:
(1)如图1, , 两点分别位于一个池塘的两端,小亮想用绳子测量 , 间的距离,但绳子不够长,聪明的小亮想出一个办法:先在地上取一个可以直接到达 点的点 ,连接 ,取 的中点 (点 可以直接到达 点),利用工具过点 作 交 的延长线于点 ,此时测得 米,那么 , 间的距离是 200 米.
思维探索:
(2)在 和 中, , ,且 , ,将 绕点 顺时针方向旋转,把点 在 边上时 的位置作为起始位置(此时点 和点 位于 的两侧),设旋转角为 ,连接 ,点 是线段 的中点,连接 , .
①如图2,当 在起始位置时,猜想: 与 的数量关系和位置关系分别是 ;
②如图3,当 时,点 落在 边上,请判断 与 的数量关系和位置关系,并证明你的结论;
③当 时,若 , ,请直接写出 的值.