把两个全等的等腰直角三角板ABC和EFG(其直角边均为4)叠放在一起(如图1),且使三角板EFG的直角顶点G与三角板ABC的斜边中点O重合,现将三角板EFG绕点O按顺时针方向旋转(旋转角α满足条件:0°<α<90°),四边形CHGK是旋转过程中两三角形的重叠部分(如图2).
在上述旋转过程中,BH与CK有怎样的数量关系?四边形CHGK的面积有何变化?请证明你的发现.
如图,在直角坐标系中,二次函数y=x2+(2k-1)x+k+1的图象与x轴相交于O、A两点。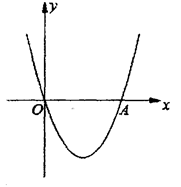
(1)求这个二次函数的解析式;
(2)在这条抛物线的对称轴右边的图象上有一点B,使△AOB的面积等于6,求点B的坐标。
为丰富学生的学习生活,某校九年级组织学生参加春游活动,所联系的旅行社收费标准如下: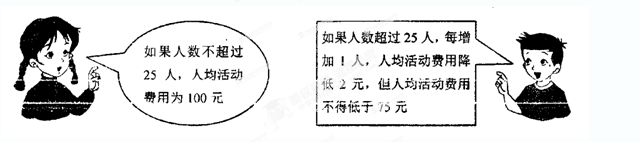
春游活动结束后,该班共支付给该旅行社活动费用2800元,请问该班共有多少人参加这次春游活动?
解方程(每题4分,共8分)
(1)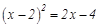
(2)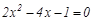
如图,在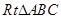 中,
中,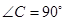 ,
,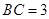 ,
,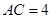 .点
.点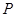 、
、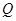 都是斜边
都是斜边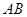 上的动点,点
上的动点,点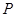 从
从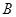 向
向 运动(不与点
运动(不与点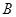 重合),点
重合),点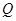 从
从 向
向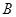 运动,
运动,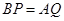 .点
.点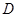 、
、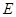 分别是点
分别是点 、
、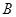 以
以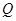 、
、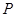 为对称中心的对称点,
为对称中心的对称点,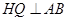 于
于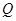 ,交
,交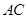 于点
于点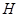 .当点
.当点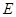 到达顶点
到达顶点 时,
时,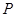 、
、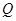 同时停止运动.设
同时停止运动.设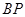 的长为
的长为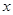 ,
,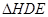 的面积为
的面积为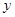 .
.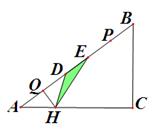
(1)求证: ∽
∽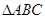 ;
;
(2)求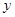 关于
关于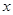 的函数解析式;
的函数解析式;
(3)当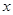 为何值时,
为何值时,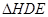 为等腰三角形?
为等腰三角形?
将 绕点
绕点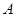 按逆时针方向旋转
按逆时针方向旋转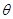 度,并使各边长变为原来的
度,并使各边长变为原来的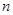 倍,得
倍,得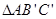 ,如图①,我们将这种变换记为
,如图①,我们将这种变换记为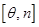 .
.
(1)如图①,对 作变换
作变换 得
得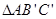 ,则
,则 ;直线
;直线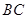 与直线
与直线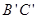 所夹的锐角为度;
所夹的锐角为度;
(2)如图②, 中,
中, ,
,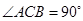 ,对
,对 作变换
作变换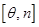 得
得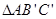 ,使点
,使点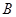 、
、 、
、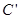 在同一直线上,且四边形
在同一直线上,且四边形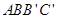 为矩形,求
为矩形,求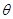 和
和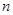 的值;
的值;
(3)如图③, 中,
中,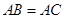 ,
, ,
,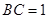 ,对
,对 作变换
作变换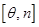 得
得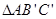 ,使点
,使点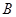 、
、 、
、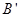 在同一直线上,且四边形
在同一直线上,且四边形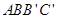 为平行四边形,求
为平行四边形,求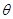 和
和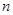 的值.
的值.