如图,在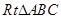 中,
中,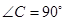 ,
,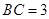 ,
,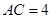 .点
.点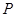 、
、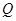 都是斜边
都是斜边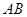 上的动点,点
上的动点,点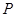 从
从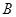 向
向 运动(不与点
运动(不与点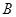 重合),点
重合),点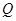 从
从 向
向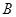 运动,
运动,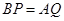 .点
.点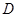 、
、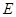 分别是点
分别是点 、
、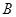 以
以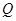 、
、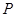 为对称中心的对称点,
为对称中心的对称点,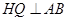 于
于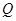 ,交
,交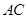 于点
于点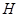 .当点
.当点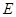 到达顶点
到达顶点 时,
时,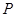 、
、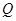 同时停止运动.设
同时停止运动.设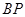 的长为
的长为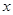 ,
,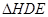 的面积为
的面积为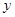 .
.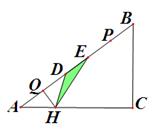
(1)求证: ∽
∽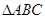 ;
;
(2)求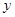 关于
关于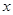 的函数解析式;
的函数解析式;
(3)当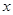 为何值时,
为何值时,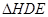 为等腰三角形?
为等腰三角形?
在边长为1的正方形网格中如图所示.
①以点 为位似中心,作出 的位似图形△ ,使其位似比为 .且△ 位于点 的异侧,并表示出 的坐标.
②作出 绕点 顺时针旋转 后的图形△ .
③在②的条件下求出点 经过的路径长.

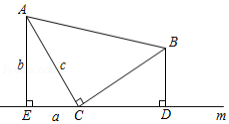
如图,等腰直角三角板如图放置.直角顶点 在直线 上,分别过点 、 作 直线 于点 , 直线 于点 .
①求证: ;
②若设 三边分别为 、 、 ,利用此图证明勾股定理.
已知实数 、 满足 ,求代数式 的值.
计算 .
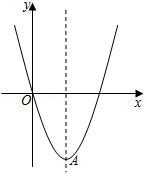
如图,在平面直角坐标系中,抛物线 经过原点 ,顶点为 .
(1)求抛物线的函数解析式;
(2)设点 为抛物线 的对称轴上的一点,点 在该抛物线上,当四边
形 为菱形时,求出点 的坐标;
(3)在(2)的条件下,抛物线 在第一象限的图象上是否存在一点 ,使得点 到直线 的距离与其到 轴的距离相等?若存在,求出直线 的函数解析式;若不存在,请说明理由.