（本小题满分10分）如图，在平面直角坐标系中，已知点B（4，2），BA⊥x轴于A．
（1）求tan∠BOA的值；
（2）在坐标系中作出将△AOB绕原点O逆时针方向旋转90°后的△COD（点A的对应点是C点，点B的对应点D点），并写出C点、D点的坐标；
（3）将△OAB平移得到△O′A′B′，点A的对应点是A′，点B的对应点B′的坐标为（2，-2），在坐标系中作出△O′A′B′，并求出平移的距离．
已知关于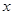
的一元二次方程
（
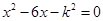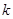为常数）．
（1）求证：方程有两个不相等的实数根；
（2）设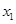
，
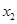为方程两个实数根，且
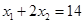，试求出方程的两个实数根和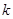的值．
先化简，再求值（1﹣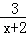
）÷
﹣
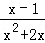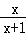，其中x满足x2+x﹣2=0．
解下列方程（本题满分8分，每小题4分）
（1） 2x2－2x－5＝0
（2）9(x＋1)2－(x－2)2＝0
如图，在以O为圆心的两个同心圆中，AB经过圆心O，且与小圆相交于点A、与大圆相交于点B．小圆的切线AC与大圆相交于点D，且CO平分∠ACB．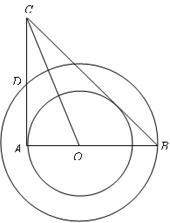
（1）试判断BC所在直线与小圆的位置关系，并说明理由；
（2）试判断线段AC、AD、BC之间的数量关系，并说明理由；
（3）若AB=8cm，BC=10cm，求大圆与小圆围成的圆环的面积．(结果保留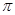
)
已知关于x的一元二次方程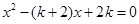
．
（1）试说明无论
取何值时，这个方程一定有实数根；
（2）若等腰△ABC的一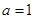边长
，另两边长
、
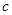恰好是这个方程的两个根 ，求△ABC的周长.