(本小题满分12分)如图,开口向下顶点为D的抛物线经过点A(0, 5),B(-1,0),C(5,0)与x轴交于B、C两点(B在C左侧),点A和点E关于抛物线对称轴对称.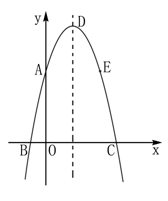
(1)求该抛物线的解析式;
(2)经过原点O和点E的直线与抛物线的另一个交点为F.
①求点F的坐标;
②求四边形ADEF的面积;
(3)若M为抛物线上一动点,N为抛物线对称轴上一动点,是否存在M,N,使得以A、E、M、N为顶点的四边形为平行四边形,若存在,求出所有满足条件的M、N的坐标;若不存在,请说明理由.
如图,AB∥CD,以点A为圆心,小于AC长为半径作圆弧,分别交AB,AC于E,F两点,再分别以E,F为圆心,大于 EF长为半径作圆弧,两条圆弧交于点P,作射线AP,交CD于点M。
EF长为半径作圆弧,两条圆弧交于点P,作射线AP,交CD于点M。
(1)若∠ACD=114°,求∠MAB的度数;
(2)若CN⊥AM,垂足为N,求证:△ACN≌△MCN。
(1)计算: ;(2)解不等式组:
;(2)解不等式组: 。
。
如图,把两个全等的Rt△AOB和Rt△COD分别置于平面直角坐标系中,使直角边OB、OD在x轴上.已知点A(1,2),过A、C两点的直线分别交x轴、y轴于点E、F.抛物线y=ax2+bx+c经过O、A、C三点.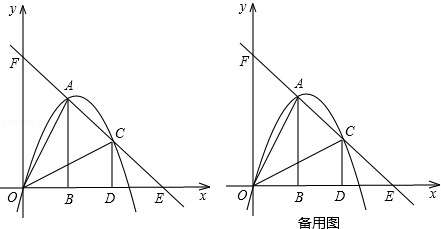
(1)求该抛物线的函数解析式;
(2)点P为线段OC上一个动点,过点P作y轴的平行线交抛物线于点M,交x轴于点N,问是否存在这样的点P,使得四边形ABPM为等腰梯形?若存在,求出此时点P的坐标;若不存在,请说明理由.
(3)若△AOB沿AC方向平移(点A始终在线段AC上,且不与点C重合),△AOB在平移过程中与△COD重叠部分面积记为S.试探究S是否存在最大值?若存在,求出这个最大值;若不存在,请说明理由.
课本中,把长与宽之比为 的矩形纸片称为标准纸.请思考解决下列问题:
的矩形纸片称为标准纸.请思考解决下列问题:
(1)将一张标准纸ABCD(AB<BC)对开,如图1所示,所得的矩形纸片ABEF是标准纸.请给予证明.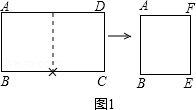
(2)在一次综合实践课上,小明尝试着将矩形纸片ABCD(AB<BC)进行如下操作:
第一步:沿过A点的直线折叠,使B点落在AD边上点F处,折痕为AE(如图2甲);
第二步:沿过D点的直线折叠,使C点落在AD边上点N处,折痕为DG(如图2乙),此时E点恰好落在AE边上的点M处;
第三步:沿直线DM折叠(如图2丙),此时点G恰好与N点重合.
请你探究:矩形纸片ABCD是否是一张标准纸?请说明理由.
(3)不难发现:将一张标准纸按如图3一次又一次对开后,所得的矩形纸片都是标准纸.现有一张标准纸ABCD,AB=1,BC= ,问第5次对开后所得标准纸的周长是多少?探索直接写出第2012次对开后所得标准纸的周长.
,问第5次对开后所得标准纸的周长是多少?探索直接写出第2012次对开后所得标准纸的周长.
在社会主义新农村建设中,衢州某乡镇决定对A、B两村之间的公路进行改造,并有甲工程队从A村向B村方向修筑,乙工程队从B村向A村方向修筑.已知甲工程队先施工3天,乙工程队再开始施工.乙工程队施工几天后因另有任务提前离开,余下的任务有甲工程队单独完成,直到公路修通.下图是甲乙两个工程队修公路的长度y(米)与施工时间x(天)之间的函数图象,请根据图象所提供的信息解答下列问题: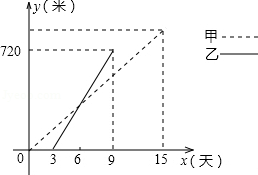
(1)乙工程队每天修公路多少米?
(2)分别求甲、乙工程队修公路的长度y(米)与施工时间x(天)之间的函数关系式.
(3)若该项工程由甲、乙两工程队一直合作施工,需几天完成?