如图甲,已知ΔABC和ΔCEF是两个不等的等边三角形,且有一个公共顶点C,连接AF和BE.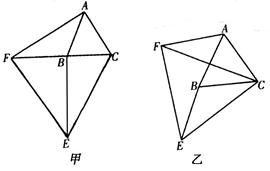
(1)线段AF和BE有怎样的大小关系?证明你的猜想.
(2)将图中的ΔCEF绕点C旋转一定的角度,得到图乙,(1)中的结论还成立吗? 做出判断并说明理由.
如图,已知反比例函数 和一次函数y=2x-1,其中一次函数的图象经过(a,b),(a+1,b+k)两点.
和一次函数y=2x-1,其中一次函数的图象经过(a,b),(a+1,b+k)两点.
(1)求反比例函数的解析式;
(2)如下图,已知点A在第一象限,且同时在上述两个函数的图象上,求点A的坐标;
(3)利用(2)的结果,请问:在x轴上是否存在点P,使△AOP为等腰三角形?若存在,把符合条件的P点坐标都求出来;若不存在,请说明理由.
在一张长12cm、宽5cm的矩形纸片内,要折出一个菱形.小华同学按照取两组对边中点的方法折出菱形EFGH(见方案一),小丽同学沿矩形的对角线AC折出∠CAE=∠CAD,∠ACF=∠ACB的方法得到菱形AECF(见方案二).
(1)你能说出小华、小丽所折出的菱形的理由吗?
(2)请你通过计算,比较小华和小丽同学的折法中,哪种菱形面积较大?
某气球内充满一定质量的气体,当温度不变时,气球内气体的气压p(kPa)是气体体积V(m3)的反比例函数,其图象如图所示.
(1)写出这一函数的表达式.
(2)当气体体积为1 m3时,气压是多少?
(3)当气球内的气压大于140 kPa时,气球将爆炸,为了安全考虑,气体的体积应不大于多少?
如图,E、F是□ABCD对角线 上的两点,且
上的两点,且 .
.
求证:(1) ;
;
(2) .
.
已知,如图,AB、DE是直立在地面上的两根立柱.AB=5m, 某一时刻AB在阳光下的投影BC=3m.
(1)请你在图中画出此时DE在阳光下的投影.
(2)在测量AB的投影时,同时测量出DE在阳光下的投影长为6m,请你计算DE的长.