如图,①请画出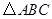 关于
关于 轴对称的
轴对称的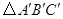 (其中
(其中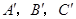 分别是
分别是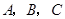 的对应点,不写画法);
的对应点,不写画法);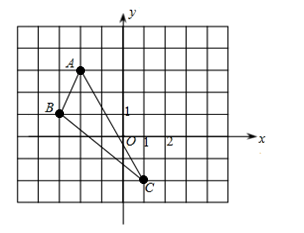
②直接写出 三点的坐标.
三点的坐标.
③在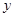 轴上找一点P使得PA+PB最小, 画出点P所在的位置(保留作图痕迹,不写画法).
轴上找一点P使得PA+PB最小, 画出点P所在的位置(保留作图痕迹,不写画法).
某学校教学楼后面紧邻着一个土坡,坡上面是一块平地,如图所示,BC∥AD,斜坡AB长22 m,坡角∠BAD=60°,为了防止山体滑坡,保障安全,学校决定对该土坡进行改造.
(1)求土坡的高度(BE)的长;
(2)经地质人员勘,测当坡角不超过45°时,可确保山体不滑坡.学校计划改造时保持坡脚A不动,坡顶B沿BC削进到F点处.求BF至少是多少米?
我区实施新课程改革后,学生的自主字习、合作交流能力有很大提高.张老师为了了解所教班级学生自主学习、合作交流的具体情况,对本班部分学生进行了为期半个月的跟踪调査,并将调査结果分成四类,A:特别好;B:好;C:一般;D:较差;并将调査结果绘制成以下两幅不完整的统计图,请你根据统计图解答下列问题:
(1)本次调查中,张老师一共调査了名同学,其中C类女生有名,D类男生有名;
(2)将上面的条形统计图补充完整;
(3)为了共同进步,张老师想从被调査的A类和D类学生中分别选取一位同学进行“一帮一”互助学习,请用列表法或画树形图的方法求出所选两位同学恰好是一位男同学和一位女同学的概率.
先化简,再求值: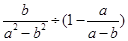 ,其中a、b是2x2-2x-7=0的根.
,其中a、b是2x2-2x-7=0的根.
如图,△ABC与△DCB中,AC与BD交于点E,且∠ABC=∠DCB,AB=DC.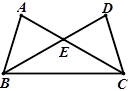
(1)求证:△ABC≌DCB;
(2)当∠EBC=30º,求∠AEB的度数?
解不等式组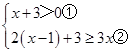 ,并在数轴上表示解集.
,并在数轴上表示解集.