如图，在平面直角坐标系中，直线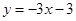
与x轴交于点A，与y轴交于点C.抛物线
经过A，C两点，且与x轴交于另一点B（点B在点A右侧）．
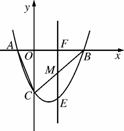
（1）求抛物线的解析式及点B坐标；
（2）若点M是线段BC上的一动点，过点M的直线EF平行y轴交x轴于点F，交抛物线于点E.求ME长的最大值；
（3）试探究当ME取最大值时，在抛物线上、x轴下方是否存在点P，使以M，F，B，P为顶点的四边形是平行四边形？若存在，请求出点P的坐标；若不存在，试说明理由．
如图，等腰梯形ABCD放置在平面直角坐标系中，已知A（-2，0）、B（6，0）、A（0，3），反比例函数的图象经过点C．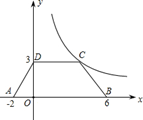
（1）求C点坐标和反比例函数的解析式；
（2）将等腰梯形ABCD向上平移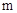
个单位后，使点B恰好落在双曲线上，求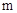的值．
如图，一次函数y=kx+b的图象与反比例函数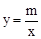
的图象交于A（-2，1），B（1，n）两点．
（1）求反比例函数和一次函数的解析式；
（2）根据图象写出使一次函数的值大于反比例函数的值的x的取值范围．
已知y－2与x成反比例，当x=3时，y=3，求y与x之间的函数关系式.
如图1，已知抛物线y=－x2+bx+c经过点A（1,0），B（－3,0）两点，且与y轴交于点C.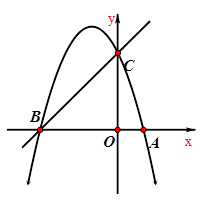
(1) 求b，c的值。
(2)在第二象限的抛物线上，是否存在一点P，使得△PBC的面积最大？求出点P的坐标及△PBC的面积最大值.若不存在，请说明理由.
(3) 如图2，点E为线段BC上一个动点（不与B,C重合），经过B、E、O三点的圆与过点B且垂直于BC的直线交于点F，当△OEF面积取得最小值时，求点E坐标．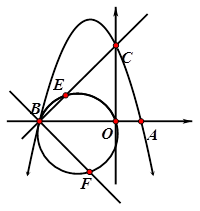
某玩具批发商销售每件进价为40元的玩具，市场调查发现，若以每件50元的价格销售，平均每天销售90件，单价每提高1元，平均每天就少销售3件．
（1）平均每天的销售量y（件）与销售价x（元/件）之间的函数关系式为 ；
（2）求该批发商平均每天的销售利润W（元）与销售价x（元/件）之间的函数关系式；
（3）物价部门规定每件售价不得高于55元，当每件玩具的销售价为多少元时，可以获得最大利润？最大利润是多少元？