小明设计了一个简易量角器：如图，在△ABC中，∠C＝90°，-优题课

小明设计了一个“简易量角器”：如图，在△ABC中，∠C＝90°，∠A＝30°，CA＝30 cm，在AB边上有一系列点P1，P2，P3…P8，使得∠P₁CA＝10°，∠P₂CA＝20°，∠P₃CA＝30°，…∠P₈CA＝80°．

（1）求P₃A的长（结果保留根号）；
（2）求P₅A的长（结果精确到1 cm，参考数据：sin50°≈0.77，cos50°≈0.64，tan50°≈1.20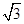，≈1.7）；
（3）小明发现P1，P2，P3…P8这些点中，相邻两点距离都不相同，于是计划用含45°的直角三角形重新制作“简易量角器”，结果会怎样呢？请你帮他继续探究．

科目数学题型解答题难度较难

知识点：解直角三角形

已知关于 $x$ 的一元二次方程 $x^{2} + (2 m + 1) x + m - 2 = 0$ ．

（1）求证：无论 $m$ 取何值，此方程总有两个不相等的实数根；

（2）若方程有两个实数根 $x_{1}$ ， $x_{2}$ ，且 $x_{1} + x_{2} + 3 x_{1} x_{2} = 1$ ，求 $m$ 的值．

先化简，再求值： $a (a + 2 b) - 2 b (a + b)$ ，其中 $a = \sqrt{5}$ ， $b = \sqrt{3}$ ．

已知抛物线 $y = a x^{2} - 2 ax + c$ 过点 $A (- 1, 0)$ 和 $C (0, 3)$ ，与 $x$ 轴交于另一点 $B$ ，顶点为 $D$ ．

（1）求抛物线的解析式，并写出 $D$ 点的坐标；

（2）如图1， $E$ 为线段 $BC$ 上方的抛物线上一点， $EF ⊥ BC$ ，垂足为 $F$ ， $EM ⊥ x$ 轴，垂足为 $M$ ，交 $BC$ 于点 $G$ ．当 $BG = CF$ 时，求 $ΔEFG$ 的面积；

（3）如图2， $AC$ 与 $BD$ 的延长线交于点 $H$ ，在 $x$ 轴上方的抛物线上是否存在点 $P$ ，使 $∠ OPB = ∠ AHB$ ？若存在，求出点 $P$ 的坐标；若不存在，请说明理由．

如图1，已知 $ΔABC ≅ ΔEBD$ ， $∠ ACB = ∠ EDB = 90 °$ ，点 $D$ 在 $AB$ 上，连接 $CD$ 并延长交 $AE$ 于点 $F$ ．

（1）猜想：线段 $AF$ 与 $EF$ 的数量关系为　　；

（2）探究：若将图1的 $ΔEBD$ 绕点 $B$ 顺时针方向旋转，当 $∠ CBE$ 小于 $180 °$ 时，得到图2，连接 $CD$ 并延长交 $AE$ 于点 $F$ ，则（1）中的结论是否还成立？若成立，请证明；若不成立，请说明理由；

（3）拓展：图1中，过点 $E$ 作 $EG ⊥ CB$ ，垂足为点 $G$ ．当 $∠ ABC$ 的大小发生变化，其它条件不变时，若 $∠ EBG = ∠ BAE$ ， $BC = 6$ ，直接写出 $AB$ 的长．

某企业接到生产一批设备的订单，要求不超过12天完成．这种设备的出厂价为1200元 $/$ 台，该企业第一天生产22台设备，第二天开始，每天比前一天多生产2台．若干天后，每台设备的生产成本将会增加，设第 $x$ 天 $(x$ 为整数）的生产成本为 $m$ （元 $/$ 台）， $m$ 与 $x$ 的关系如图所示．

（1）若第 $x$ 天可以生产这种设备 $y$ 台，则 $y$ 与 $x$ 的函数关系式为　 $y = 2 x + 20$ 　， $x$ 的取值范围为　　；

（2）第几天时，该企业当天的销售利润最大？最大利润为多少？

（3）求当天销售利润低于10800元的天数．

试卷网试题网古诗词网作文网范文网