在函数中,我们规定:当自变量增加一个单位时,因变量的增加量称为函数的平均变化率.例如,对于函数y=3x+1,当自变量x增加1时,因变量y=3(x+1)+1=3x+4,较之前增加3,故函数y=3x+1的平均变化率为3.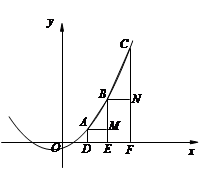
(1)①列车已行驶的路程s(km)与行驶的时间t(h)的函数关系式是s=300t,该函数的平均变化率是 ;其蕴含的实际意义是 ;
②飞机着陆后滑行的距离y(m)与滑行的时间x(s)的函数关系式是y=-1.5x2+60x,求该函数的平均变化率;
(2)通过比较(1)中不同函数的平均变化率,你有什么发现;
(3)如图,二次函数y=ax2+bx+c的图像经过第一象限内的三点A、B、C,过点A、B、C作x轴的垂线,垂足分别为D、E、F,AM⊥BE,垂足为M,BN⊥CF,垂足为N,DE=EF,试探究△AMB与△BNC面积的大小关系,并说明理由.
将正方形 的边 绕点 逆时针旋转至 ,记旋转角为 ,连接 ,过点 作 垂直于直线 ,垂足为点 ,连接 , .
(1)如图1,当 时, 的形状为 ,连接 ,可求出 的值为 ;
(2)当 且 时,
①(1)中的两个结论是否仍然成立?如果成立,请仅就图2的情形进行证明;如果不成立,请说明理由;
②当以点 , , , 为顶点的四边形是平行四边形时,请直接写出 的值.

小亮在学习中遇到这样一个问题:
如图,点 是 上一动点,线段 ,点 是线段 的中点,过点 作 ,交 的延长线于点 .当 为等腰三角形时,求线段 的长度.
小亮分析发现,此问题很难通过常规的推理计算彻底解决,于是尝试结合学习函数的经验研究此问题.请将下面的探究过程补充完整:
(1)根据点 在 上的不同位置,画出相应的图形,测量线段 , , 的长度,得到下表的几组对应值.
|
|
0 |
1.0 |
2.0 |
3.0 |
4.0 |
5.0 |
6.0 |
7.0 |
8.0 |
|
|
8.0 |
7.7 |
7.2 |
6.6 |
5.9 |
|
3.9 |
2.4 |
0 |
|
|
8.0 |
7.4 |
6.9 |
6.5 |
6.1 |
6.0 |
6.2 |
6.7 |
8.0 |
操作中发现:
①“当点 为 的中点时, ”.则上表中 的值是 5.0 ;
②“线段 的长度无需测量即可得到”.请简要说明理由.
(2)将线段 的长度作为自变量 , 和 的长度都是 的函数,分别记为 和 ,并在平面直角坐标系 中画出了函数 的图象,如图所示.请在同一坐标系中画出函数 的图象;
(3)继续在同一坐标系中画出所需的函数图象,并结合图象直接写出:当 为等腰三角形时,线段 长度的近似值(结果保留一位小数).


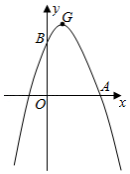
如图,抛物线 与 轴正半轴, 轴正半轴分别交于点 , ,且 ,点 为抛物线的顶点.
(1)求抛物线的解析式及点 的坐标;
(2)点 , 为抛物线上两点(点 在点 的左侧),且到对称轴的距离分别为3个单位长度和5个单位长度,点 为抛物线上点 , 之间(含点 , 的一个动点,求点 的纵坐标 的取值范围.
我们学习过利用尺规作图平分一个任意角,而“利用尺规作图三等分一个任意角”曾是数学史上一大难题,之后被数学家证明是不可能完成的.人们根据实际需要,发明了一种简易操作工具 三分角器.图1是它的示意图,其中 与半圆 的直径 在同一直线上,且 的长度与半圆的半径相等; 与 垂直于点 , 足够长.

使用方法如图2所示,若要把 三等分,只需适当放置三分角器,使 经过 的顶点 ,点 落在边 上,半圆 与另一边 恰好相切,切点为 ,则 , 就把 三等分了.
为了说明这一方法的正确性,需要对其进行证明.如下给出了不完整的“已知”和“求证”,请补充完整,并写出“证明”过程.
已知:如图2,点 , , , 在同一直线上, ,垂足为点 , .
求证: .
暑期将至,某健身俱乐部面向学生推出暑期优惠活动,活动方案如下.
方案一:购买一张学生暑期专享卡,每次健身费用按六折优惠;
方案二:不购买学生暑期专享卡,每次健身费用按八折优惠.
设某学生暑期健身 (次 ,按照方案一所需费用为 (元 ,且 ;按照方案二所需费用为 (元 ,且 .其函数图象如图所示.
(1)求 和 的值,并说明它们的实际意义;
(2)求打折前的每次健身费用和 的值;
(3)八年级学生小华计划暑期前往该俱乐部健身8次,应选择哪种方案所需费用更少?说明理由.
