若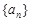 是各项均不为零的等差数列,公差为
是各项均不为零的等差数列,公差为 ,
, 为其前
为其前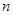 项和,且满足
项和,且满足 ,
, .数列
.数列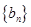 满足
满足 ,
,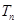 为数列
为数列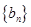 的前
的前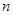 项和.
项和.
(Ⅰ)求 和
和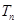 ;
;
(Ⅱ)是否存在正整数 ,使得
,使得 成等比数列?若存在,求出所有
成等比数列?若存在,求出所有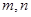 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
在直角坐标系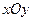 中,以
中,以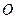 极点,
极点,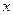 轴正半轴为极轴建立极坐标系,曲线C的极坐标方程为
轴正半轴为极轴建立极坐标系,曲线C的极坐标方程为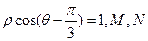 分别为
分别为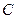 与
与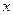 轴,
轴,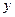 轴的交点
轴的交点
(1)写出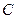 的直角坐标方程,并求出
的直角坐标方程,并求出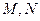 的极坐标
的极坐标
(2)设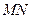 的中点为
的中点为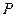 ,求直线
,求直线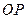 的极坐标方程
的极坐标方程
双曲线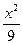 -
-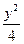 =1与直线y=kx-1只有一个公共点,求k的值.
=1与直线y=kx-1只有一个公共点,求k的值.
已知两个向量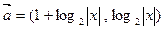 ,
,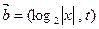
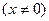 .
.
(1)若t=1且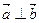 ,求实数x的值;
,求实数x的值;
(2)对tÎR写出函数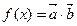 具备的性质.
具备的性质.
设 表示幂函数
表示幂函数 在
在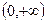 上是增函数的
上是增函数的 的集合;
的集合;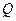 表示不等式
表示不等式 对任意
对任意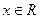 恒成立的
恒成立的 的集合。(1)求
的集合。(1)求 ;(2)试写出一个解集为
;(2)试写出一个解集为 的不等式。
的不等式。
已知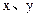 之间满足
之间满足
(1)方程 表示的曲线经过一点
表示的曲线经过一点 ,求b的值
,求b的值
(2)动点(x,y)在曲线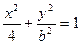 (b>0)上变化,求x2+2y的最大值;
(b>0)上变化,求x2+2y的最大值;
(3)由 能否确定一个函数关系式
能否确定一个函数关系式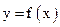 ,如能,求解析式;如不能,再加什么条件就可使
,如能,求解析式;如不能,再加什么条件就可使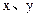 之间建立函数关系,并求出解析式。
之间建立函数关系,并求出解析式。
(