设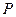 表示幂函数
表示幂函数 在
在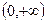 上是增函数的
上是增函数的 的集合;
的集合;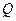 表示不等式
表示不等式  对任意
对任意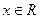 恒成立的
恒成立的 的集合。(1)求
的集合。(1)求 ;(2)试写出一个解集为
;(2)试写出一个解集为 的不等式。
的不等式。
(本小题满分12分)设函数 .
.
(1)写出 的最大值M,最小值m,最小正周期T;
的最大值M,最小值m,最小正周期T;
(2)试求最小正整数k,使得当自变量x在任意两个整数间(包括整数本身)变化时,函数 至少有一个值是M和一个值是m .
至少有一个值是M和一个值是m .
(本小题满分12分)
某市地铁全线共有四个车站,甲、乙两人同时在地铁第一号车站(首发站)乘车.假设每人自第2号车站开始,在每个车站下车是等可能的。约定用有序实数对 表示“甲在
表示“甲在 号车站下车,乙在
号车站下车,乙在 号车站下车”。
号车站下车”。
(Ⅰ)用有序实数对把甲、乙两人下车的所有可能的结果列举出来;
(Ⅱ)求甲、乙两人同在第3号车站下车的概率;
(Ⅲ)求甲、乙两人在不同的车站下车的概率。
(本小题满分12分)为了了解小学生的体能情况,抽取了某小学同年级部分学生进行跳绳测试,将所得数据整理后,画出频率分布直方图如图所示,已知图中从左到右前三个小组的频率分别是0.1,0.3,0.4,第一小组的频数为5.
(1)求第四小组的频率;
(2)参加这次测试的学生人数是多少?
(3)在这次测试中,学生跳绳次数的中位数落在第几小组内?
(本小题满分10分)已知


 (I)化简
(I)化简
(II)若 是第三象限角,且
是第三象限角,且 ,求
,求 的值。
的值。
已知椭圆 的两个焦点分别为F1(-c,0),F2(c
的两个焦点分别为F1(-c,0),F2(c ,0),(c>0),过点E
,0),(c>0),过点E 的直线与椭圆交于A、B两点,且F1A//F2B,|F1A|=2|F2B|,
的直线与椭圆交于A、B两点,且F1A//F2B,|F1A|=2|F2B|,
(1)求离心率;
( 2)求直线AB的斜率;
2)求直线AB的斜率;
(3)设点C与点A关于标标原点对称,直线F2B上有一点H(m,n)(m≠0)在△AF1C的外接圆上,求 的值。
的值。