（本小题满分10分）在△ABC中，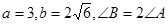
.
（1）求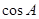
的值， （2）求
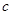的值
已知二次函数y＝f（x）的图象经过坐标原点，其导函数f ′（x）＝2x＋2，数列{an}的前n项和为Sn，点（n，Sn）（n∈N*）均在函数y＝f（x）的图象上．
（1）求数列{an}的通项公式；
（2）设bn＝2n·an，Tn是数列{bn}的前n项和，求Tn．
在△ABC中，a、b、c分别是角A、B、C的对边，向量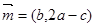
，
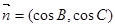，且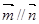
（1）求角B的大小；
（2）设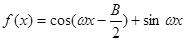
（
），且f（x）的最小正周期为π，求f（x）的单调区间．
已知函数f（x）的定义域是（0，＋∞），当x>1时，f（x）>0，且f（x·y）＝f（x）＋f（y）．
（1）证明：f（x）在定义域上是增函数；
（2）如果f（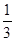
）＝－1，求满足不等式f（x）－f（
）≥2的x的取值范围．
若函数f（x）＝－x3＋6x2－9x＋m在区间[0,4]上的最小值为2，求它在该区间上的最大值．
在△ABC中，角A，B，C的对边分别为a，b，c，且满足（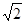
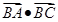a－c）
＝c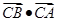 
（1）求角B的大小；
（2）若|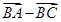
|＝
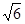，求△ABC面积的最大值．