(本小题满分12分)某人上午7:00乘汽车以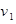 千米/小时
千米/小时 匀速从A地出发到距300公里的B地,在B地不作停留,然后骑摩托车以
匀速从A地出发到距300公里的B地,在B地不作停留,然后骑摩托车以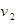 千米/小时
千米/小时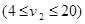 匀速从B地出发到距50公里的C地,计划在当天16:00至21:00到达C地。设乘汽车、骑摩托车的时间分别是x,y小时,如果已知所需的经费
匀速从B地出发到距50公里的C地,计划在当天16:00至21:00到达C地。设乘汽车、骑摩托车的时间分别是x,y小时,如果已知所需的经费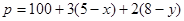 元,那么
元,那么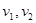 分别是多少时走的最经济,此时花费多少元?
分别是多少时走的最经济,此时花费多少元?
(本小题满分14分)函数 ,
, .
.
(Ⅰ)当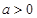 时,求函数
时,求函数 的单调区间和极大值;
的单调区间和极大值;
(Ⅱ)当 时,讨论方程
时,讨论方程 解得个数;
解得个数;
(Ⅲ)求证: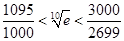 (参考数据:
(参考数据: ).
).
(本小题满分13分)已知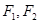 是椭圆
是椭圆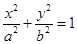 的左、右焦点,
的左、右焦点, 为坐标原点,点
为坐标原点,点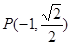 在椭圆上,线段
在椭圆上,线段 与
与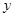 轴的交点
轴的交点 满足
满足
(1)求椭圆的标准方程;
(2)⊙ 是以
是以 为直径的圆,一直线
为直径的圆,一直线 与⊙
与⊙ 相切,并与椭圆交于不同的两点
相切,并与椭圆交于不同的两点 .当
.当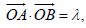 ,且满足
,且满足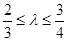 时,求
时,求 面积
面积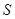 的取值范围.
的取值范围.
(本小题满分12分)已知数列 的前
的前 和
和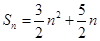 ,数列
,数列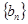 的通项公式
的通项公式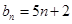 .
.
(1)求数列 的通项公式;
的通项公式;
(2)设 ,求证:
,求证: ;
;
(本小题满分12分)如图,在四棱锥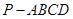 中, 四边形
中, 四边形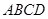 是直角梯形,
是直角梯形,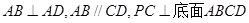 ,
, 是
是 的中点.
的中点.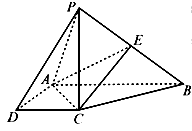
(Ⅰ)求证:平面 ⊥平面
⊥平面 ;
;
(Ⅱ)若二面角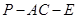 的余弦值为
的余弦值为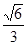 ,求直线
,求直线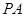 与平面
与平面 所成角的正弦值.
所成角的正弦值.
(本小题满分12分)甲乙两班进行消防安全知识竞赛,每班出 人组成甲乙两支代表队,首轮比赛每人一道必答题,答对则为本队得
人组成甲乙两支代表队,首轮比赛每人一道必答题,答对则为本队得 分,答错不答都得
分,答错不答都得 分,已知甲队
分,已知甲队 人每人答对的概率分别为
人每人答对的概率分别为 ,乙队每人答对的概率都是
,乙队每人答对的概率都是 .设每人回答正确与否相互之间没有影响,用
.设每人回答正确与否相互之间没有影响,用 表示甲队总得分.
表示甲队总得分.
(Ⅰ)求随机变量 的分布列及其数学期望
的分布列及其数学期望 ;
;
(Ⅱ)求在甲队和乙队得分之和为 的条件下,甲队比乙队得分高的概率.
的条件下,甲队比乙队得分高的概率.