(本小题满分12分)甲乙两班进行消防安全知识竞赛,每班出 人组成甲乙两支代表队,首轮比赛每人一道必答题,答对则为本队得
人组成甲乙两支代表队,首轮比赛每人一道必答题,答对则为本队得 分,答错不答都得
分,答错不答都得 分,已知甲队
分,已知甲队 人每人答对的概率分别为
人每人答对的概率分别为 ,乙队每人答对的概率都是
,乙队每人答对的概率都是 .设每人回答正确与否相互之间没有影响,用
.设每人回答正确与否相互之间没有影响,用 表示甲队总得分.
表示甲队总得分.
(Ⅰ)求随机变量 的分布列及其数学期望
的分布列及其数学期望 ;
;
(Ⅱ)求在甲队和乙队得分之和为 的条件下,甲队比乙队得分高的概率.
的条件下,甲队比乙队得分高的概率.
在△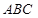 中,
中,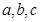 分别为三个内角
分别为三个内角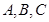 的对边,
的对边,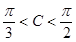 ,且
,且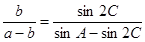 .
.
(Ⅰ) 判断△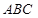 的形状;
的形状;
(Ⅱ) 若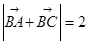 ,求
,求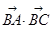 的取值范围.
的取值范围.
某市电视台为了宣传举办问答活动,随机对该市15~65岁的人群抽样了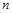 人,回答问题统计结果如图表所示.
人,回答问题统计结果如图表所示.
| 组号 |
分组 |
回答正确 的人数 |
回答正确的人数 占本组的概率 |
| 第1组 |
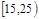 |
5 |
0.5 |
| 第2组 |
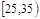 |
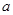 |
0.9 |
| 第3组 |
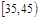 |
27 |
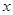 |
| 第4组 |
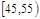 |
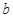 |
0.36 |
| 第5组 |
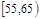 |
3 |
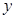 |
(Ⅰ) 分别求出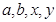 的值;
的值;
(Ⅱ) 从第2,3,4组回答正确的人中用分层抽样的方法抽取6人,则第2,3,4组每组应各抽取多少人?
(Ⅲ) 在(Ⅱ)的前提下,电视台决定在所抽取的6人中随机抽取2人颁发幸运奖,求:所抽取的人中第2组至少有1人获得幸运奖的概率.
已知向量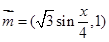 ,
,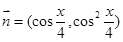 ,
,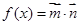
(Ⅰ)若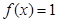 ,求
,求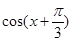 的值;
的值;
(Ⅱ)在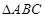 中,角
中,角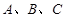 的对边分别是
的对边分别是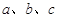 ,且满足
,且满足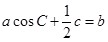 ,求函数
,求函数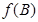 的取值范围.
的取值范围.
从某批产品中,有放回地抽取产品二次,每次随机抽取1件,假设事件 :“取出的2件产品中至多有1件是二等品”的概率
:“取出的2件产品中至多有1件是二等品”的概率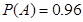 .
.
(Ⅰ) 求从该批产品中任取1件是二等品的概率 ;
;
(Ⅱ) 若该批产品共100件,从中依次抽取2件,求事件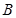 :“取出的2件产品中至少有一件二等品”的概率
:“取出的2件产品中至少有一件二等品”的概率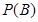 .
.
已知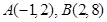 .
.
(Ⅰ)若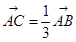 ,
,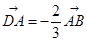 ,求
,求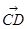 的坐标;
的坐标;
(Ⅱ)设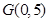 ,若
,若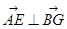 ,
, ∥
∥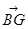 ,求
,求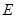 点坐标.
点坐标.