(本小题满分l3分)某大学志愿者协会有6窑男同学,4名女同学,在这10名同学中,3名同学自数学学院,其余7名同学
自物理、化学等其他互不相同的7个学院,现从这10名同学中随机选取3名同学,到希望小学进行支教活
动(每位同学被选到的可能性相同).
(1)求选出的3名同学是自互不相同学院的概率:
(2)设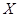 为选出的3名同学中女同学的人数,求随机变量
为选出的3名同学中女同学的人数,求随机变量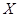 的分布列和数学期望.
的分布列和数学期望.
如图所示,在四棱锥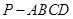 中,底面
中,底面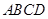 为矩
为矩
形,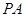 ⊥平面
⊥平面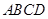 ,
, ,
,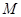 为
为 上的点,若
上的点,若 ⊥平面
⊥平面
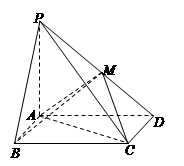
(1)求证: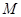 为
为 的中点;
的中点;
(2)求二面角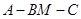 的大小.
的大小.
设函数 .
.
(1)求f(x)的单调区间;
(2)若当x∈[-2,2]时,不等式f(x)>m恒成立,求实数m的取值范围.
在△ABC中,角A,B,C的对边分别为a,b,c,cos  =
= .
.
(1)求cosB的值;
(2)若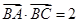 ,b=2
,b=2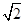 ,求a和c的值.
,求a和c的值.
如图,在边长为1的正方形OABC内取一点P(x,y),求: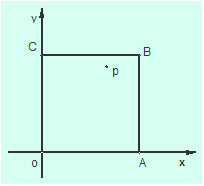
(1)点P到原点距离小于1的概率;
(2)以x,y,1为边长能构成三角形的概率;
(3)以x,y,1为边长能构成锐角三角形的概率
如图,A地到火车站共有两条路径L1,L2,现随机抽取100位从A地到火车站的人进行调查,结果如下:
| 所用时间(min) |
10~20 |
20~30 |
30~40 |
40~50 |
50~60 |
| 选择L1人数 |
6 |
12 |
18 |
12 |
12 |
| 选择L2人数 |
0 |
4 |
16 |
16 |
4 |
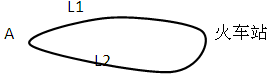
(1)试估计40 min内不能赶到火车站的概率
(2)现甲有40 min时间赶往火车站,为尽最大可能在允许的时间内赶到火车站,试通过计算说明,他如何选路径