如图,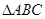 是等腰直角三角形,
是等腰直角三角形,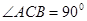 ,
, ,
,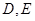 分别为
分别为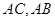 的中点,沿
的中点,沿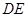 将
将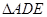 折起,得到如图所示的四棱锥
折起,得到如图所示的四棱锥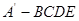 .
.
(Ⅰ)在棱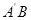 上找一点
上找一点 ,使
,使 ∥平面
∥平面 ;
;
(Ⅱ)当四棱锥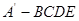 的体积取最大值时,求平面
的体积取最大值时,求平面 与平面
与平面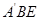 夹角的余弦值.
夹角的余弦值.
已知函数 .
.
(Ⅰ)用分段函数的形式表示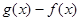 ,并求
,并求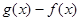 的最大值;
的最大值;
(Ⅱ)若 ,求实数
,求实数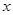 的取值范围.
的取值范围.
(本题满分12分)我国是水资源匮乏的国家,为鼓励节约用水,某市打算出台一项水费政策措施.规定:每季度每人用水量不超过5吨时,每吨水费收基本价1.3元;若超过5吨而不超过6吨时,超过部分的水费按基本价3倍收取;若超过6吨而不超过7吨时,超过部分的水费按基本价5倍收取.
某人本季度实际用水量为 吨,应交水费为
吨,应交水费为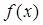 元。
元。
(Ⅰ)求 的值;
的值;
(Ⅱ)试求出函数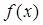 的解析式.
的解析式.
已知函数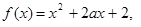
(Ⅰ)若 在
在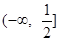 是减函数,在
是减函数,在 是增函数,求实数
是增函数,求实数 的值;
的值;
(Ⅱ)求实数 的取值范围,使
的取值范围,使 在区间
在区间 上是单调函数,并指出相应的单调性.
上是单调函数,并指出相应的单调性.
已知函数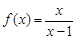 ,
,
(Ⅰ)求 的定义域和值域;
的定义域和值域;
(Ⅱ)判断函数 在区间(2,5)上的单调性,并用定义来证明所得结论.
在区间(2,5)上的单调性,并用定义来证明所得结论.
已知二次函数 的最小值为-1,且
的最小值为-1,且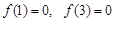 ,
,
(Ⅰ)求 的值;
的值;
(Ⅱ)求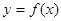 在
在 上的单调区间与值域.
上的单调区间与值域.