如图,三棱柱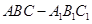 中,侧棱垂直底面,
中,侧棱垂直底面, ,
, ,
,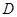 是棱
是棱 的中点。
的中点。
(1)证明: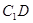 ⊥平面
⊥平面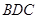
(2)设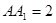 ,求几何体
,求几何体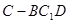 的体积。
的体积。
求函数f(x)=x(5-2x)2 的最大值.
的最大值.
某房地产开发公司计划在一楼区内建造一个长方形公园ABCD,公园由长方形休闲区A1B1C1D1和环公园人行道(阴影部分)组成.已知休闲区A1B1C1D1的面积为4000平方米,人行道的宽分别为4米和10米(如图所示).
(1)若设休闲区的长和宽的比 =x,求公园ABCD所占面积S关于x的函数解析式.
=x,求公园ABCD所占面积S关于x的函数解析式.
(2)要使公园所占面积最小,休闲区A1B1C1D1的长和宽应如何设计?
已知a,b,x,y∈R+,x,y为变量,a,b为常数,且a+b=10, +
+ =1,x+y的最小值为18,求a,b.
=1,x+y的最小值为18,求a,b.
已知a,b,c均为正数,且a+b+c=1,求证: +
+ +
+ ≥9.
≥9.
已知a,b,x,y都是正数,且a+b=1,求证:(ax+by)(bx+ay)≥xy.