6本不同的书,按以下要求各有多少种分法?
(1)平均分成三组;
(2)分成1本,2本、3本三组;
(3)平均分给甲、乙、丙三人;
(4)分给甲、乙、丙三人,一人拿1本,一人拿2本、一人拿3本;
(5)甲得一本,乙得二本,丙得三本.
(本小题满分12分)已知 ,计算:
,计算:
(1) ;(2)
;(2)
(本小题满分12分)已知双曲线 的左、右焦点分别为
的左、右焦点分别为 ,
, ,过点
,过点 的动直线与双曲线相交于
的动直线与双曲线相交于 两点.
两点.
(1)若动点 满足
满足 (其中
(其中 为坐标原点),求点
为坐标原点),求点 的轨迹方程;
的轨迹方程;
(2)在 轴上是否存在定点
轴上是否存在定点 ,使
,使 ·
· 为常数?若存在,求出点
为常数?若存在,求出点 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
(本小题满分12分)设 .
.
(1)若 在
在 上存在单调递增区间,求
上存在单调递增区间,求 的取值范围;
的取值范围;
(2)当 时,
时, 在
在 上的最小值为
上的最小值为 ,求
,求 在该区间上的最大值.
在该区间上的最大值.
(本小题满分12分)在举办的环境保护知识有奖问答比赛中,甲、乙、丙同时回答一道有关环境保护知识的问题,已知甲回答对这道题目的概率是 ,甲、丙两人都回答错的概率是
,甲、丙两人都回答错的概率是 ,乙、丙两人都回答对的概率是
,乙、丙两人都回答对的概率是 .
.
(1)求乙、丙两人各自回答对这道题目的概率.
(2)求甲、乙、丙三人中至少有两人回答对这道题目的概率.
(本小题满分12分)如图,四棱锥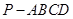 中,底面
中,底面 为矩形,
为矩形, 底面
底面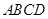 ,
,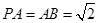 ,点
,点 是棱
是棱 的中点.
的中点.
(1)证明: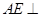 平面
平面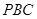 ;
;
(2)若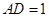 ,求二面角
,求二面角 的平面角的余弦值.
的平面角的余弦值.