某食品厂为了检查一条自动包装流水线的生产情况,随机抽取该流水线上40件产品作为样本称出它们的重量(单位:克),重量的分组区间为(490,495],(495,500],…,(510,515],由此得到样本的频率分布直方图,如图所示.
(1)根据频率分布直方图,求重量超过505克的产品数量;
(2)在上述抽取的40件产品中任取2件,设Y为重量超过505克的产品数量,求Y的分布列;
(3)从该流水线上任取5件产品,求恰有2件产品的重量超过505克的概率.
已知函数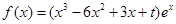 ,
, .
.
(1)若函数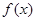 在点
在点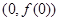 处的切线方程为
处的切线方程为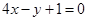 ,求
,求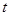 的值;
的值;
(2)若函数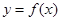 有三个不同的极值点,求
有三个不同的极值点,求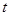 的值;
的值;
(3)若存在实数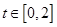 ,使对任意的
,使对任意的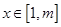 ,不等式
,不等式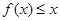 恒成立,求正整数
恒成立,求正整数 的最大值.
的最大值.
已知抛物线 上点
上点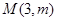 到焦点
到焦点 的距离为4.
的距离为4.
(1)求抛物线方程;
(2)点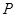 为准线上任意一点,
为准线上任意一点,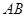 为抛物线上过焦点的任意一条弦(如图),设直线
为抛物线上过焦点的任意一条弦(如图),设直线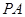 ,
,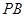 ,
,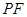 的斜率为
的斜率为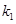 ,
,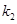 ,
,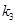 ,问是否存在实数
,问是否存在实数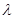 ,使得
,使得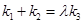 恒成立.若存在,请求出
恒成立.若存在,请求出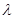 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.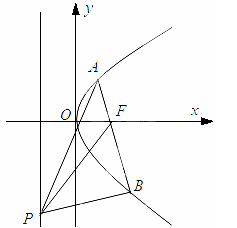
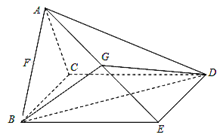
如图,四棱锥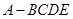 ,平面
,平面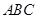 ⊥平面
⊥平面 ,△
,△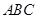 是边长为2的等边三角形,底面
是边长为2的等边三角形,底面 是矩形,且
是矩形,且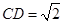 .
.
(1)若点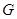 是
是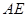 的中点,求证:
的中点,求证: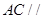 平面
平面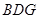 ;
;
(2)若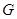 为
为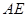 上任意一点,试问点
上任意一点,试问点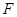 在线段
在线段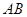 上什么位置时,
上什么位置时,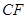 ⊥
⊥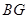 ;
;
(3)若点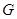 是
是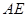 的中点,求
的中点,求 .
.
在数学趣味知识培训活动中,甲乙两名学生的5次培训成绩如茎叶图所示: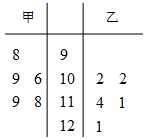
(1)从甲、乙两人中选择1人参加数学趣味知识竞赛,你会选哪位?请运用统计学的知识说明理由;
(2)从乙的5次培训成绩中随机选择2个,试求选到121分的概率.
在等差数列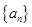 中,
中,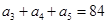 ,
,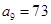 .
.
(1)求数列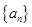 的通项公式;
的通项公式;
(2)对任意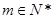 ,将数列
,将数列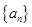 中落入区间
中落入区间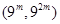 内的项的个数记为
内的项的个数记为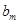 ,求数列
,求数列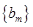 的前
的前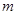 项和
项和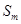 .
.