(本小题共14分)已知函数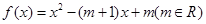 。
。
(1)若 为方程
为方程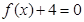 的两个实根,并且A,B为锐角,
的两个实根,并且A,B为锐角, 求m的取值范围;
求m的取值范围;
(2)对任意实数 ,恒有
,恒有 ,证明:
,证明: .
.
已知函数
(1)求函数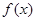 的最小正周期及在区间
的最小正周期及在区间
 上的最大值和最小值;
上的最大值和最小值;
(2)若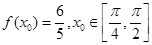 ,求
,求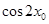 的值。
的值。
(本小题满分12分)设函数 .
.
(1)判断函数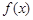 的奇偶性,并写出
的奇偶性,并写出 时
时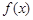 的单调增区间;
的单调增区间;
(2)若方程 有解,求实数
有解,求实数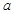 的取值范围.
的取值范围.
(本题满分15分) 已知函数f (x)=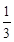 x3+ax2+bx, a , b
x3+ax2+bx, a , b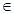 R.
R.
(Ⅰ) 曲线C:y=f (x) 经过点P (1,2),且曲线C在点P处的切线平行于直线y=2x+1,求a,b的值;
(Ⅱ) 已知f (x )在区间 (1,2) 内存在两个极值点,求证:0<a+b<2.
)在区间 (1,2) 内存在两个极值点,求证:0<a+b<2.
(本小题共15分)已知函数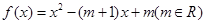 。
。
(1)若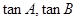 为
为 方程
方程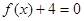 的两个实根,并且A,B为锐角,求m的取值范围;
的两个实根,并且A,B为锐角,求m的取值范围;
(2)对任意实数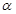 ,恒有
,恒有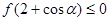 ,证明:
,证明: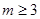 .
.