已知函数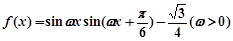 ,且其图象的相邻对称轴间的距离为
,且其图象的相邻对称轴间的距离为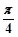 .
.
(I)求 在区间
在区间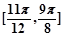 上的值域;
上的值域;
(II)在锐角 中,若
中,若
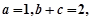 求
求 的面积.
的面积.
已知A(-2,0),B(2,0),动点P与A、B两点连线的斜率分别为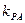 和
和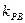 ,且满足
,且满足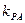 ·
·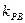 ="t" (t≠0且t≠-1). 当t<0时,曲线C的两焦点为F1,F2,若曲线C上存在点Q使得∠F1QF2=120O,求t的取值范围.
="t" (t≠0且t≠-1). 当t<0时,曲线C的两焦点为F1,F2,若曲线C上存在点Q使得∠F1QF2=120O,求t的取值范围.
已知A(-2,0),B(2,0),动点P与A、B两点连线的斜率分别为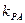 和
和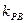 ,且满足
,且满足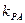 ·
·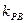 ="t" (t≠0且t≠-1).求动点P的轨迹C的方程.
="t" (t≠0且t≠-1).求动点P的轨迹C的方程.
设双曲线方程为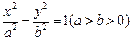 ,P为双曲线上任意一点,F为双曲线的一个焦点,讨论以|PF|为直径的圆与圆x2+y2=a2的位置关系.
,P为双曲线上任意一点,F为双曲线的一个焦点,讨论以|PF|为直径的圆与圆x2+y2=a2的位置关系.
设F1、F2为曲线C1∶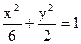 的焦点,P是曲线C2∶
的焦点,P是曲线C2∶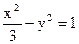 与C1的一个交点,求的值.
与C1的一个交点,求的值.
垂直于x轴的直线交双曲线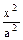 -
-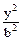 =1右支于M,N两点,A1,A2为双曲线的左右两个顶点,求直线A1M与A2N的交点P的轨迹方程,并指出轨迹的形状.
=1右支于M,N两点,A1,A2为双曲线的左右两个顶点,求直线A1M与A2N的交点P的轨迹方程,并指出轨迹的形状.