(本小题满分12分)设函数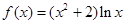 ,
,
(1)证明: 是
是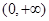 上的增函数;
上的增函数;
(2)设 ,当
,当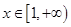 时,
时, 恒成立,求
恒成立,求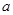 的取值范围.
的取值范围.
已知函数 (其中
(其中 )的图象与x轴在原点右侧的第一个交点为N(6,0),又
)的图象与x轴在原点右侧的第一个交点为N(6,0),又
(1)求这个函数解析式
(2)设关于x的方程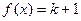 在[0,8]内有两个不同根
在[0,8]内有两个不同根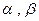 ,求
,求 的值及k的取值范围。
的值及k的取值范围。
设排球队A与B进行比赛,规定若有一队胜四场,则为获胜队,已知两队水平相当
(1)求A队第一、五场输,第二、三、四场赢,最终获胜的概率;
(2)若要决出胜负,平均需要比赛几场?
(1)解关于x的不等式
(2)记a>0时(1)中不等式的解集为A,集合B= ,若
,若 恰有3个元素,求a的取值范围。
恰有3个元素,求a的取值范围。
设 ,
,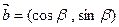
(1)若 ,
, 为
为 与
与 的夹角,求
的夹角,求 。
。
(2)若 与
与 夹角为60o,那么t为何值时
夹角为60o,那么t为何值时 的值最小?
的值最小?
(本小题满分14分)已知抛物线 ,椭圆经过点
,椭圆经过点 ,它们在
,它们在 轴上有共同焦点,椭圆的对称轴是坐标轴.(Ⅰ)求椭圆的方程;(Ⅱ)若
轴上有共同焦点,椭圆的对称轴是坐标轴.(Ⅰ)求椭圆的方程;(Ⅱ)若 是椭圆上的点,设
是椭圆上的点,设 的坐标为
的坐标为 (
(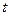 是已知正实数),求
是已知正实数),求 与
与 之间的最短距离.
之间的最短距离.