(本小题满分12分)已知函数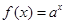 的图象过点
的图象过点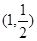 ,且点
,且点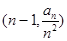
 在函数
在函数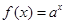 的图象上.
的图象上.
(1)求数列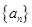 的通项公式;
的通项公式;
(2)令 ,若数列
,若数列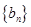 的前
的前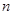 项和为
项和为 ,求证:
,求证: .
.
计划展出10幅不同的画,其中1幅水彩画,4幅油画,5幅国画,排成一行陈列,要求同一品种的画必须放在一起,并且水彩画不放在两端,不同的陈列种数有多少种?
2个男生和4个女生排成一排,其中男生既不相邻也不排两端的不同排法共有多少种?
已知数列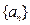 中,
中,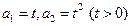 。
。
若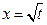 是函数
是函数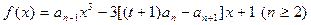 的一个极值点。
的一个极值点。
(1)求数列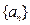 的通项公式;
的通项公式;
(2)若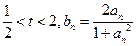 ,求证:对于任意正整数
,求证:对于任意正整数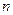 ,
,
都有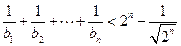 ;
;
(3)若 ,证明:
,证明: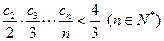
已知等比数列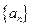 ,
,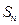 是其前
是其前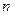 项的和,且
项的和,且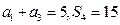 .
.
(1)求数列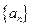 的通项公式;
的通项公式;
(2)设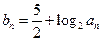 ,求数列
,求数列 的前
的前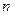 项和
项和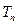 ;
;
甲、乙两个篮球运动员相互没有影 响地站在罚球线上投球,其中甲的命中率为
响地站在罚球线上投球,其中甲的命中率为 ,乙的命中率为
,乙的命中率为 ,现在每人都投球三次,且各次投球的结果互不影响.求:
,现在每人都投球三次,且各次投球的结果互不影响.求:
(1)甲恰好投进两球 的概率
的概率 ;
;
(2)甲乙两人都恰好投进两球的概率;